题目内容
已知四棱锥 中,侧棱
中,侧棱 底面
底面 ,且底面
,且底面 是边长为2的正方形,
是边长为2的正方形, ,
, 与
与 相交于点
相交于点 .
.

(I)证明: ;
;
(II)求三棱锥 的体积.
的体积.
 中,侧棱
中,侧棱 底面
底面 ,且底面
,且底面 是边长为2的正方形,
是边长为2的正方形, ,
, 与
与 相交于点
相交于点 .
.
(I)证明:
 ;
;(II)求三棱锥
 的体积.
的体积.(I)详见试题解析;(II) .
.
 .
.试题分析:(I)要证
 与
与 垂直,只要证明
垂直,只要证明 平面
平面 .
. 平面
平面 ,又
,又 ,且
,且 与
与 交于点
交于点 ,
, 平面
平面 或者证明三角形
或者证明三角形 为等腰三角形,可以通过证明直角三角形
为等腰三角形,可以通过证明直角三角形 和直角三角形
和直角三角形 全等证得
全等证得 ;(II)可以直接利用棱锥体积计算公式:
;(II)可以直接利用棱锥体积计算公式: 直接求三棱锥
直接求三棱锥 的体积,也可利用等体积法转化为求
的体积,也可利用等体积法转化为求 ,这样底面积
,这样底面积 易求,而三棱锥
易求,而三棱锥 高即为
高即为 ,可以利用线面垂直的证法证得.
,可以利用线面垂直的证法证得.试题解析:(I)证明:
 平面
平面 ,又
,又 ,且
,且 与
与 交于点
交于点 ,
, 平面
平面
 平面
平面 6分
6分(II)解:
 底面
底面 平面
平面
 13分
13分
练习册系列答案
 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
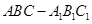 中,
中,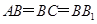 ,
,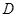 为
为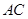 的中点.
的中点.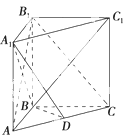
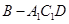 的体积.
的体积. ,这个长方体的顶点都在同一个球面上,则这个球的表面积为( )
,这个长方体的顶点都在同一个球面上,则这个球的表面积为( )



 倍,则球的半径扩大到原来的 倍,球的体积扩大到原来的 倍.( )
倍,则球的半径扩大到原来的 倍,球的体积扩大到原来的 倍.( ) 、
、
 S2
S2 和
和 ,较短腰长为
,较短腰长为










