题目内容
设椭圆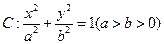 过点
过点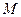 (
(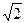
 ,1),且左焦点为
,1),且左焦点为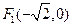 .
.
(1)求椭圆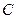 的方程;
的方程;
(2)判断是否存在经过定点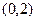 的直线
的直线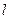 与椭圆
与椭圆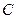 交于
交于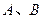 两点并且满足
两点并且满足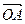 ·
·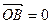 ,若存在求出直线
,若存在求出直线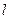 的方程,不存在说明理由.
的方程,不存在说明理由.
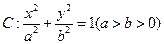 过点
过点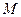 (
(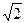
 ,1),且左焦点为
,1),且左焦点为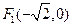 .
.(1)求椭圆
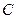 的方程;
的方程;(2)判断是否存在经过定点
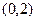 的直线
的直线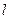 与椭圆
与椭圆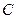 交于
交于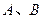 两点并且满足
两点并且满足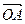 ·
·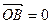 ,若存在求出直线
,若存在求出直线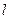 的方程,不存在说明理由.
的方程,不存在说明理由.(1)

(2)
 (存在)
(存在)略

练习册系列答案
相关题目
题目内容
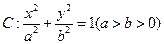 过点
过点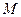 (
(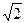
 ,1),且左焦点为
,1),且左焦点为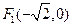 .
.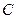 的方程;
的方程;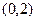 的直线
的直线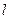 与椭圆
与椭圆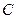 交于
交于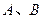 两点并且满足
两点并且满足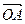 ·
·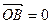 ,若存在求出直线
,若存在求出直线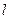 的方程,不存在说明理由.
的方程,不存在说明理由.
 (存在)
(存在)