题目内容

9．七个同学参加三个兴趣小组，每人只能参加一个兴趣小组，每个兴趣小组至少两个同学，则不同的参加方法有（　　）
A．630种B．210种C．420种D．1890种

分析 由题意可知，只能分为（2，2，3）一组，分组后再分配到三个兴趣小组，问题得以解决．

解答 解：七个同学参加三个兴趣小组，每人只能参加一个兴趣小组，每个兴趣小组至少两个同学，则7个同学只能分为（2，2，3），分组后再分配到三个兴趣小组，故有$\frac{{C}_{7}^{3}•{C}_{4}^{2}}{{A}_{2}^{2}}•{A}_{3}^{3}$=630种，
故选：A．

点评 本题考查了分组分配的问题，关键是如何分组，属于中档题．

练习册系列答案
相关题目
9．已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{\sqrt{2}}{2}$．且左右顶点分别为A（一1，0）、B（1，0）．
（1）求椭圆的标准方程；
（2）过椭圆的右焦点F且倾斜角为$\frac{π}{4}$的直线l交椭圆于C、D两点，|CF|=λ|DF|（|CF|＞|DF|），求λ的值；
（3）过P（-$\frac{5}{3}$，0）的直线交椭圆于M、N两点（异于A、B两点），记直线AM、AN 的斜率分别为k1、k2，问k1与K2的乘积是否为定值？若为定值，请说明理由．
10．用100万元炒股，第一天涨停板（涨10%），第二天跌停板（跌10%），那么第二天实际亏了1万元．
7．用lgx，lgy，lgz，lg（x+y），lg（x-y）表示下列各式（其中x＞y＞0，z＞0）：
（1）lg（xyz）；
（2）lg（xy-2z-1）；
（3）lg（x2y2z-3）；
（4）lg$\frac{\sqrt{x}}{{y}^{3}z}$；
（5）lg$\frac{xy}{（{x}^{2}-{y}^{2}）}$；
（6）lg（$\frac{x+y}{x-y}$•y）；
（7）lg[$\frac{y}{x（x-y）}$]3．
4．在实数集R中，我们定义的大小关系“＞”为全体实数排了一个“序”．类似实数排序的定义，我们定义“点序”记为“＞”：已知M（x1，y1）和N（x2，y2），M＞N，当且仅当“x1＞x2”或“x1=x2且y1＞y2”．定义两点的“⊕”与“?”运算如下：M⊕N=（x1+x2，y1+y2）    M?N=x1x2+y1y2．则下面四个命题：
①已知P（2015，2014）和Q（2014，2015），则P＞Q；
②已知P（2015，2014）和Q（x，y），若P＞Q，则x≤2015，且y≤2014；
③已知P＞Q，Q＞M，则P＞M；
④已知P＞Q，则对任意的点M，都有P⊕M＞Q⊕M；
⑤已知P＞Q，则对任意的点M，都有P?M＞Q?M．
其中真命题的序号为①③④（把真命题的序号全部写出）．
14．执行如图所示的程序框图，输出的S值为（　　）
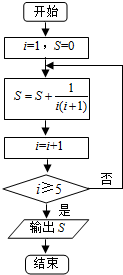
A．$\frac{4}{5}$B．$\frac{3}{4}$C．$\frac{5}{6}$D．1
1．将正整数从1开始依次写下来，直至2015为止，得到一个新的正整数：1234…201320142015．这个正整数是几位数（　　）
A．3506位数B．4518位数C．6953位数D．7045位数
18．如图中的程序框图所描述的算法称为欧几里得辗转相除法．若输入m=459，n=357，则输出m=（　　）
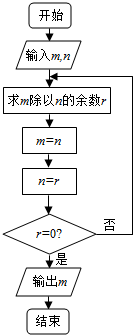
A．51B．17C．9D．3
19．图是一个算法的流程图，则输出的n=9．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网