题目内容
若双曲线的右焦点F到一条渐近线的距离是点F到右顶点的距离与点F到中心的距离的等差中项,则离心率e=
- A.

- B.

- C.

- D.

A
分析:根据双曲线的标准方程,算出右焦点F到一条渐近线的距离为b,结合题意得c-a、b、c成等差数列,由此可得2b=2c-a,平方后根据b2=c2-a2化简整理,得5a=4c,由此即可算出该双曲线的离心率.
解答: 设双曲线方程为
设双曲线方程为 -
- =1(a>0,b>0)
=1(a>0,b>0)
可得双曲线的渐近线方程为bx±ay=0,
∴右焦点F到一条渐近线的距离为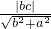 =b
=b
因此c-a、b、c成等差数列,
∴2b=(c-a)+c,平方得4b2=(2c-a)2
∵b2=c2-a2,
∴4c2-4a2=4c2-4ac+a2,整理得5a=4c
因此,该双曲线的离心率e= =
=
故选:A
点评:本题给出双曲线右焦点F到一条渐近线的距离是点F到右顶点的距离与点F到中心的距离的等差中项,求双曲线的离心率.着重考查了双曲线的标准方程和简单几何性质等知识,属于基础题.
分析:根据双曲线的标准方程,算出右焦点F到一条渐近线的距离为b,结合题意得c-a、b、c成等差数列,由此可得2b=2c-a,平方后根据b2=c2-a2化简整理,得5a=4c,由此即可算出该双曲线的离心率.
解答:
 设双曲线方程为
设双曲线方程为 -
- =1(a>0,b>0)
=1(a>0,b>0)可得双曲线的渐近线方程为bx±ay=0,
∴右焦点F到一条渐近线的距离为
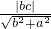 =b
=b因此c-a、b、c成等差数列,
∴2b=(c-a)+c,平方得4b2=(2c-a)2
∵b2=c2-a2,
∴4c2-4a2=4c2-4ac+a2,整理得5a=4c
因此,该双曲线的离心率e=
 =
=
故选:A
点评:本题给出双曲线右焦点F到一条渐近线的距离是点F到右顶点的距离与点F到中心的距离的等差中项,求双曲线的离心率.着重考查了双曲线的标准方程和简单几何性质等知识,属于基础题.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
 的右焦点F与圆C:x2-4x+y2-6=0的圆心重合,点F到双曲线的一条渐近线的距离为1,则双曲线的离心率为
的右焦点F与圆C:x2-4x+y2-6=0的圆心重合,点F到双曲线的一条渐近线的距离为1,则双曲线的离心率为









