题目内容
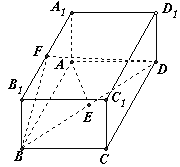
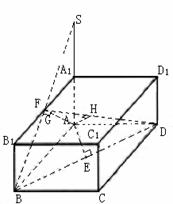
(20)如图,已知长方体![]()
![]() 直线
直线![]() 与平面
与平面
![]() 所成的角为
所成的角为![]() ,
,![]() 垂直
垂直![]() 于
于![]() ,
,![]() 为
为![]() 的中点.
的中点.
(I)求异面直线![]() 与
与![]() 所成的角;
所成的角;
(II)求平面![]() 与平面
与平面![]() 所成的二面角(锐角)的大小;
所成的二面角(锐角)的大小;
(III)求点![]() 到平面
到平面![]() 的距离.
的距离.
20、
解法一:在长方体![]() 中,以
中,以![]() 所在的直线为
所在的直线为![]() 轴,以
轴,以![]() 所在的直线为
所在的直线为![]() 轴,
轴,![]() 所在的直线为
所在的直线为![]() 轴建立空间直角坐标系如图。
轴建立空间直角坐标系如图。

由已知![]() 可得
可得![]()
![]() 。
。
又![]() 平面
平面![]() ,从而
,从而![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,
,
又![]() ,
,![]() ,
,![]() 。
。
从而易得 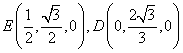 …………
…………
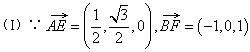
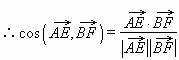
= 。
。
即异面直线![]() 所成的角为
所成的角为![]() 。
。
(II)易知平面![]() 的一个法向量m=(0,1,0).
的一个法向量m=(0,1,0).
设n=(x,y,z)是平面![]() 的一个法向量,
的一个法向量,
![]()
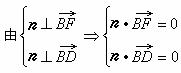
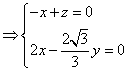
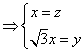 ,
,
即n=(1,![]() ,1),…………………………
,1),…………………………
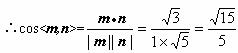
即平面![]() 与平面
与平面![]() 所成的二面角的大小(锐角)为
所成的二面角的大小(锐角)为![]()
(III)点![]() 到平面
到平面![]() 的距离,即
的距离,即![]() 在平面
在平面![]() 的法向量n上的投影的绝对值,
的法向量n上的投影的绝对值,
所以距离
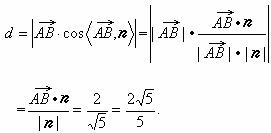
所以点![]() 到平面
到平面![]() 的距离为
的距离为![]() 。
。
解法二:(I)连结![]() ,过
,过![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() 。
。

∵![]() 与两底面
与两底面![]() 都垂直,
都垂直,
∴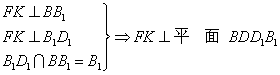
又 平面
平面![]()
因此![]() ∥
∥![]() 。
。
∴![]() 为异面直线
为异面直线![]() 与
与![]() 所成的角。……………………
所成的角。……………………
连结![]() ,由FK⊥BDD1B1得
,由FK⊥BDD1B1得![]() ,
,
从而![]() 为Rt△。
为Rt△。
在![]() 和
和![]() 中,
中,
由![]() 得
得
 ,
,
又![]() ,
,
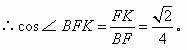
∴异面直线![]() 所成的角为
所成的角为![]() 。……………………
。……………………
(II)由于![]() ,由
,由![]() 作
作![]() 的垂线
的垂线![]() ,垂足为
,垂足为![]() ,连结
,连结![]() ,由三垂线定理知
,由三垂线定理知![]() 。
。
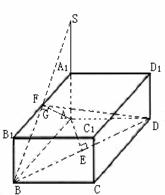
∴![]() 即为平面
即为平面![]() 与平面
与平面![]() 所成二面角,且
所成二面角,且![]() ,在平面
,在平面![]() 中,延长
中,延长![]() 与
与![]() 交于点
交于点![]() 。
。
∵![]() 为
为![]() 的中点,
的中点,![]() ∥
∥![]() 且
且![]() ,
,
∴![]() 分别为
分别为![]() 的中点,
的中点,
即![]() ,
,
∴![]() 为等腰直角三角形,垂足
为等腰直角三角形,垂足![]() 点实为斜边
点实为斜边![]() 的中点
的中点![]() ,即
,即![]() 重合。
重合。
易得![]() 。在
。在![]() 中,
中,![]() ,
,
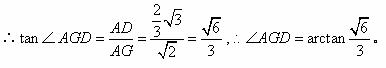
即平面![]() 与平面
与平面![]() 所成的二面角的大小(锐角)为
所成的二面角的大小(锐角)为![]() 。
。
(III)由(II)知平面![]() 是平面
是平面![]() 与平面
与平面![]() 所成二面角的平面角所在的平面,
所成二面角的平面角所在的平面,
∴面![]() 面
面![]() 。
。
在![]() 中,由
中,由![]() 作
作![]() 于
于![]() ,则
,则![]() 即为
即为![]() 点到平面
点到平面![]() 的距离。
的距离。
由![]() ,得
,得
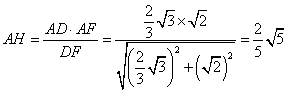 。
。
所以点![]() 到平面
到平面![]() 的距离为
的距离为![]() 。
。

练习册系列答案
相关题目
 在A、B、C、D四小题中只能选做2题,每小题10分,共计20分,请在答题纸指定区域内作答,解答应写出文字说明、证明过程或演算步骤.
在A、B、C、D四小题中只能选做2题,每小题10分,共计20分,请在答题纸指定区域内作答,解答应写出文字说明、证明过程或演算步骤. 如图,
如图, 是边长为
是边长为 的正方形,以
的正方形,以 为圆心,
为圆心, 为半径的圆弧与以
为半径的圆弧与以 为直径的半⊙O交于点
为直径的半⊙O交于点 ,延长
,延长 交
交 于
于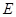 .
. 的长.
的长. ,其中
,其中 ,若点
,若点 在矩阵A的变换下得到
在矩阵A的变换下得到 .
. 的极坐标方程为
的极坐标方程为 ,
,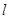 与圆相交于
与圆相交于 ,A两点,且∠
,A两点,且∠ ,求
,求 的长.
的长. ,且与圆相切的直线的极坐标方程;
,且与圆相切的直线的极坐标方程; 满足
满足 ,求
,求 的最小值;
的最小值; 如图,
如图, 是边长为
是边长为 的正方形,以
的正方形,以 为圆心,
为圆心, 为半径的圆弧与以
为半径的圆弧与以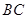 为直径的半⊙O交于点
为直径的半⊙O交于点 ,延长
,延长 交
交 于
于 .
. 的长.
的长. ,其中
,其中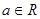 ,若点
,若点 在矩阵A的变换下得到
在矩阵A的变换下得到 .
. 的极坐标方程为
的极坐标方程为 ,
, 与圆相交于
与圆相交于 ,A两点,且∠
,A两点,且∠ ,求
,求 的长.
的长. ,且与圆相切的直线的极坐标方程;
,且与圆相切的直线的极坐标方程; 满足
满足 ,求
,求 的最小值;
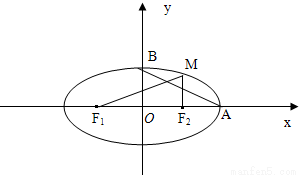
的最小值; 如图,已知椭圆
如图,已知椭圆 (a>b>0),M为椭圆上的一个动点,F1、F2分别为椭圆的左、右焦点,A、B分别为椭圆的一个长轴端点与短轴的端点.当MF2⊥F1F2时,原点O到直线MF1的距离为
(a>b>0),M为椭圆上的一个动点,F1、F2分别为椭圆的左、右焦点,A、B分别为椭圆的一个长轴端点与短轴的端点.当MF2⊥F1F2时,原点O到直线MF1的距离为 |OF1|.
|OF1|. 时,求此时椭圆的方程;
时,求此时椭圆的方程; .
. (a>b>0),M为椭圆上的一个动点,F1、F2分别为椭圆的左、右焦点,A、B分别为椭圆的一个长轴端点与短轴的端点.当MF2⊥F1F2时,原点O到直线MF1的距离为
(a>b>0),M为椭圆上的一个动点,F1、F2分别为椭圆的左、右焦点,A、B分别为椭圆的一个长轴端点与短轴的端点.当MF2⊥F1F2时,原点O到直线MF1的距离为 |OF1|.
|OF1|. 时,求此时椭圆的方程;
时,求此时椭圆的方程;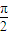 .
.