题目内容
解关于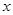 的不等式
的不等式 .
.
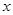 的不等式
的不等式 .
.
(1)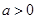 时,原不等式可化为
时,原不等式可化为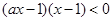 即
即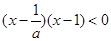
对应方程两根为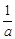 和1,
和1,
当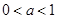 时,
时, 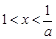 , 此时原不等式解集为
, 此时原不等式解集为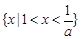
当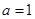 时,
时, 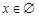 , 此时原不等式解集为
, 此时原不等式解集为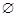
当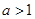 时,
时,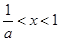 . 此时原不等式解集为
. 此时原不等式解集为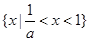
(2)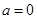 时,原不等式可化为
时,原不等式可化为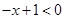 , 解得
, 解得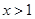 ,
,
此时原不等式解集为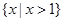
(3)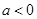 时
时
原不等式可化为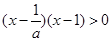 ,对应方程两根为
,对应方程两根为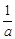 和1,
和1,
解得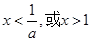 , 此时原不等式解集为
, 此时原不等式解集为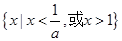
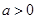 时,原不等式可化为
时,原不等式可化为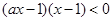 即
即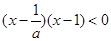
对应方程两根为
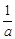 和1,
和1, 当
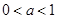 时,
时, 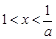 , 此时原不等式解集为
, 此时原不等式解集为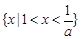
当
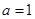 时,
时, 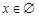 , 此时原不等式解集为
, 此时原不等式解集为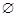
当
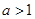 时,
时,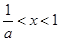 . 此时原不等式解集为
. 此时原不等式解集为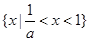
(2)
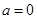 时,原不等式可化为
时,原不等式可化为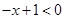 , 解得
, 解得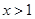 ,
, 此时原不等式解集为
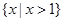
(3)
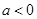 时
时原不等式可化为
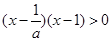 ,对应方程两根为
,对应方程两根为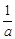 和1,
和1,解得
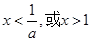 , 此时原不等式解集为
, 此时原不等式解集为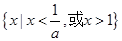
本试题主要是考查了一元二次不等式的求解的运用,需要对开口方向做出讨论,然后结合根的大小关系表示解集的综合运用。

练习册系列答案
相关题目
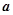 ,
,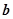 ,
,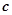 均为正实数,且
均为正实数,且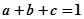 ,求证:
,求证: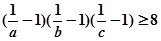 .
.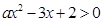 的解集为
的解集为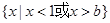
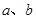 ;
;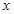 的不等式
的不等式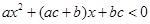 .
.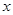 的不等式
的不等式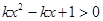 恒成立,则实数k的取值范围是__________________.
恒成立,则实数k的取值范围是__________________.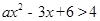 的解集为
的解集为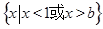
 (1)求
(1)求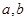 的值;
的值;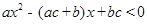
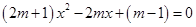 有一正根和一负根,则实数
有一正根和一负根,则实数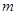 的取值范围( )
的取值范围( )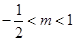


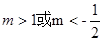
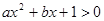 的解集为
的解集为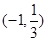 ,则
,则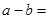 .
.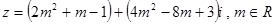 ,当实数m取什么值时,复数z:
,当实数m取什么值时,复数z: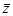 对应的点在第一象限。
对应的点在第一象限。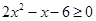 的解集为
的解集为