题目内容
已知集合A={x|x2-4ax+
思路解析一:由A∩B≠![]() 可知,方程x2-4ax+
可知,方程x2-4ax+
解法一:∵A∩B≠![]() ,B={x|x<0},
,B={x|x<0},
∴方程x2-4ax+
(1)当方程x2-4ax+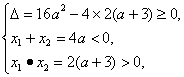
即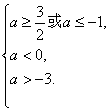 解得-3<a≤-1.
解得-3<a≤-1.
(2)当方程x2-4ax+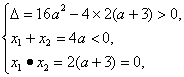
解得a=-3.
(3)当方程x2-4ax+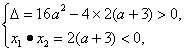
解得a<-3.
综上所述,所求实数a的取值范围为a≤-1.
思路解析二:如果从反面考虑,先求出方程x2-4ax+
解法二:设全集U={a|Δ=(![]() )≥0}={a|a≤-1或a≥
)≥0}={a|a≤-1或a≥![]() }.若方程x2-4ax+
}.若方程x2-4ax+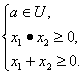 解得a≥
解得a≥![]() .在全集U中,集合{a|a≥
.在全集U中,集合{a|a≥![]() }的补集为{a|a≤-1}.∴所求实数a的取值范围是a≤-1.
}的补集为{a|a≤-1}.∴所求实数a的取值范围是a≤-1.

练习册系列答案
相关题目