题目内容

（选修4-1几何证明选讲）如图所示，AB和AC分别是圆O的切线，且OC=3，AB=4，延长AO与圆O交于D点，则△ABD的面积是
48
5
48
5
．
分析：利用圆的切线的性质及三角形的面积即可得出．
解答：解：∵AB是圆O的切线，∴OB⊥AB．
作BE⊥AD，垂足为E．
又OC═OB=3，AB=4，∴AO=
32+42
=5．
∴BE=
OB•BA
OA
=
12
5
．
∴△ABD的面积S=
1
2
AD×BE=
1
2
×(5+3)×
12
5
=
48
5
．
故答案为
48
5
．
点评：熟练掌握圆的切线的性质及三角形的面积是解题的关键．
练习册系列答案
相关题目
精英家教网A．（选修4-4坐标系与参数方程）已知点A是曲线ρ=2sinθ上任意一点，则点A到直线ρsin(θ+
π3
)=4的距离的最小值是
 
．
B．（选修4-5不等式选讲）不等式|x-log2x|＜x+|log2x|的解集是
 
．
C．（选修4-1几何证明选讲）如图所示，AC和AB分别是圆O的切线，且OC=3，AB=4，延长AO到D点，则△ABD的面积是
 
．
（2012•石家庄一模）选修4-1几何证明选讲
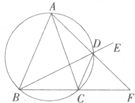已知△ABC中AB=AC，D为△ABC外接圆劣弧，
AC
上的点（不与点A、C重合），延长BD至E，延长AD交BC的延长线于F．
（I）求证．∠CDF=∠EDF
（II）求证：AB•AC•DF=AD•FC•FB．
（2013•辽宁）（选修4-1几何证明选讲）
如图，AB为⊙O的直径，直线CD与⊙O相切于E，AD垂直CD于D，BC垂直CD于C，EF垂直于AB于F，连接AE，BE，证明：
（1）∠FEB=∠CEB；
（2）EF2=AD•BC．
（考生注意：请在下列三题中任选一题作答，如果多做，则按所做的第一题评阅记分）
（A）（选修4-4坐标系与参数方程）已知点A是曲线ρ=2sinθ上任意一点，则点A到直线ρsin(θ+
π
3
)=4的距离的最小值是
5
2
5
2
．
（B）（选修4-5不等式选讲）已知2x+y=1，x＞0，y＞0，则
x+2y
xy
的最小值是
9
9
．
（C）（选修4-1几何证明选讲）若直角△ABC的内切圆与斜边AB相切于点D，且AD=1，BD=2，则△ABC的面积为
2
2
．
（2011•南京模拟）A．选修4-1几何证明选讲
如图，△ABC的外接圆的切线AE与BC的延长线相交于点E，∠BAC的平分线与BC交于点D．
求证：ED2=EB•EC．
B．矩阵与变换
已知矩阵A=
2-1
-43
，
4-1
-31
，求满足AX=B的二阶矩阵X．
C．选修4-4 参数方程与极坐标
若两条曲线的极坐标方程分别为ρ=1与ρ=2cos（θ+
π
3
），它们相交于A，B两点，求线段AB的长．
D．选修4-5 不等式证明选讲设a，b，c为正实数，求证：a3+b3+c3+
1
abc
≥2
3
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网