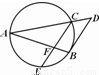
题目内容
①(不等式选讲选做题)若不等式|x+1|+|x-2|<a无实数解,则a的取值范围是 .②(极坐标参数方程选做题)曲线
 ,(α为参数)与曲线ρ2-2ρcosθ=0的交点个数为 个.
,(α为参数)与曲线ρ2-2ρcosθ=0的交点个数为 个.
【答案】分析:①根据|x+1|+|x-2|的几何意义可得其最小值等于3,可得当a≤3时,|x+1|+|x-2|<a无实数解.
②把参数方程化为普通方程,把极坐标方程化为直角坐标方程,根据两圆的圆心距大于两圆的半径之差小于两圆的半径之和,即可得到两圆是相交的位置关系.
解答:解:①|x+1|+|x-2|表示数轴上的x到2和-1对应点的距离之和,其最小值等于3,
故当a≤3时,关于x的不等式|x+1|+|x-2|<a无实数解,
故答案为:a≤3.
②由题设知:把参数方程消去参数化为普通方程得 x2+(y-1)2=1,
把极坐标方程化为直角方程得 x2+y2-2x=0,即(x-1)2+y2=1;
两圆心距为 ,且
,且  ,故两圆相交,故有2个公共点.
,故两圆相交,故有2个公共点.
故答案为 2.
点评:①本小题考查绝对值的意义,绝对值不等式的解法,函数的恒成立问题,求得|x+1|+|x-2|的最小值等于1,是解题的关键.
②本题考查把参数方程化为普通方程的方法,把极坐标方程化为普通方程的方法,由两圆的圆心距大于两圆的半径之差小于两圆的半径之和,即可得到两圆相交.
②把参数方程化为普通方程,把极坐标方程化为直角坐标方程,根据两圆的圆心距大于两圆的半径之差小于两圆的半径之和,即可得到两圆是相交的位置关系.
解答:解:①|x+1|+|x-2|表示数轴上的x到2和-1对应点的距离之和,其最小值等于3,
故当a≤3时,关于x的不等式|x+1|+|x-2|<a无实数解,
故答案为:a≤3.
②由题设知:把参数方程消去参数化为普通方程得 x2+(y-1)2=1,
把极坐标方程化为直角方程得 x2+y2-2x=0,即(x-1)2+y2=1;
两圆心距为
 ,且
,且  ,故两圆相交,故有2个公共点.
,故两圆相交,故有2个公共点.故答案为 2.
点评:①本小题考查绝对值的意义,绝对值不等式的解法,函数的恒成立问题,求得|x+1|+|x-2|的最小值等于1,是解题的关键.
②本题考查把参数方程化为普通方程的方法,把极坐标方程化为普通方程的方法,由两圆的圆心距大于两圆的半径之差小于两圆的半径之和,即可得到两圆相交.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案
相关题目
 ,则线段CD的长为 .
,则线段CD的长为 .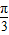 )的直角坐标是 .
)的直角坐标是 .
 ,则线段CD的长为 .
,则线段CD的长为 . )的直角坐标是 .
)的直角坐标是 .
 ,则线段CD的长为 .
,则线段CD的长为 . )的直角坐标是 .
)的直角坐标是 .
 ,则线段CD的长为 .
,则线段CD的长为 .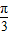 )的直角坐标是 .
)的直角坐标是 .
 ,则线段CD的长为 .
,则线段CD的长为 . )的直角坐标是 .
)的直角坐标是 .