题目内容
已知函数
，在曲线y＝f(x)的所有切线中，有且仅有一条切线l与直线2x＋y＝0平行．
(Ⅰ)求a的值及切线l的方程；
(Ⅱ)求函数f(x)的极大值和极小值．
答案：
解析：
解析：
|
(Ⅰ)∵切线l与直线 2x＋y＝0平行， ∴f′(x)＝ax2＋4x＋2＝－2，即ax2＋4x＋4＝0． 2分 又这样的切线l仅有一条， ∴△16－16＝0，得a＝1． 将a＝1代入ax2＋4x＋4＝0，得x＝－2． 从而y＝ 故 (Ⅱ)f′(x)＝x2＋4x＋2 由f′(x)＞0，得x＜－2－ ∴函数f(x)在(－∞，－2－ －2＋ 故f(x)极大＝f(－2－ f(x)极小＝f(－2＋ |
，即切点坐标为(－2，
：y－
或x＞－2＋
和[－2＋
上单调增，在[－2－
练习册系列答案
寒假学与练系列答案
相关题目
，求实数a的值；
．
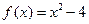，设曲线y＝f（x）在点（xn，f（xn））处的切线与x轴的交点为（xn+1,0）（n ÎN *），x1＝4．
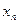表示xn+1；
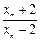，证明数列｛an｝成等比数列，并求数列｛xn｝的通项公式；
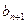与
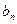的大小．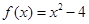
，设曲线y＝f（x）在点（xn，f（xn））处的切线与x轴的交点为（xn+1,0）（n Î N *），x1＝4．
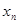表示xn+1；
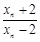，证明数列｛an｝成等比数列，并求数列｛xn｝的通项公式；
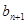与
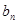的大小．