题目内容
18.设数列{an}满足an+1+an-1≤2an(n∈N*,n≥2),则称数列{an}为凸数列,已知等差数列{bn}的公差为lnd,首项b1=2,且数列{$\frac{{b}_{n}}{n}$}为凸数列,则d的取值范围是( )| A. | (0,e2] | B. | [e2,+∞) | C. | (2,e2] | D. | [2,+∞) |
分析 等差数列{bn}的公差为lnd,首项b1=2,可得bn,$\frac{{b}_{n}}{n}$=$\frac{2-lnd}{n}$+lnd.由数列{$\frac{{b}_{n}}{n}$}为凸数列,可得$\frac{2-lnd}{n+1}+lnd+\frac{2-lnd}{n-1}+lnd$≤2$(\frac{2-lnd}{n}+lnd)$,化简整理解出即可.
解答 解:∵等差数列{bn}的公差为lnd,首项b1=2,
∴bn=2+(n-1)lnd.
∴$\frac{{b}_{n}}{n}$=$\frac{2-lnd}{n}$+lnd,
∵数列{$\frac{{b}_{n}}{n}$}为凸数列,
∴$\frac{2-lnd}{n+1}+lnd+\frac{2-lnd}{n-1}+lnd$≤2$(\frac{2-lnd}{n}+lnd)$,
化为(2-lnd)$(\frac{1}{n+1}+\frac{1}{n-1}-\frac{2}{n})$≤0,
∴2-lnd≤0,
解得d≥e2.
故选:B.
点评 本题考查了新定义、等差数列的通项公式、对数函数的单调性、不等式的解法,考查了变形能力、推理能力与计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.已知tanα,tanβ是关于x的方程x2+(logaM+logbM)x-logaM•logbM=0两个根,其中a,b,M均不为1的正数,若sinαcosβ+cosαsinβ=2sinαsinβ,则a,b,M满足的关系是( )
| A. | $\frac{a+b}{2}$=M | B. | $\sqrt{ab}$=M | C. | a+b=M | D. | ab=M |
9.如图,在长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=1,则点C到平面BC1D的距离等于( )
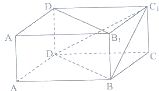

| A. | $\sqrt{6}$ | B. | $\frac{\sqrt{6}}{2}$ | C. | $\frac{\sqrt{6}}{3}$ | D. | $\frac{\sqrt{6}}{9}$ |
10.函数f(x)=x2-1,则f(1)=( )
| A. | 1 | B. | 0 | C. | -1 | D. | 2 |
 如图,抛物线C的顶点为坐标原点,焦点F为圆x2+(y-1)2=1的圆心.
如图,抛物线C的顶点为坐标原点,焦点F为圆x2+(y-1)2=1的圆心.