题目内容
公比为 的等比数列
的等比数列 的各项都是正数,且
的各项都是正数,且 ,则
,则 = ( )
= ( )
A. | B. | C. | D. |
B
解析试题分析:由等比数列性质知, =
= ,由
,由 是各项都是正数且公比为2的等比数列求得
是各项都是正数且公比为2的等比数列求得 =4,∴
=4,∴ =
= =2.
=2.
考点:等比数列性质

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
等比数列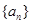 中,
中,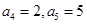 ,则数列
,则数列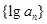 的前8项和等于( )
的前8项和等于( )
| A.6 | B.5 | C.4 | D.3 |
设 为等比数列
为等比数列 的前n项和,已知
的前n项和,已知
 ,则公比q = ( ).
,则公比q = ( ).
| A.3 | B.4 | C.5 | D.6 |
已知 ,
,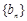 都是等比数列,它们的前
都是等比数列,它们的前 项和分别为
项和分别为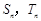 ,且
,且 ,对
,对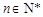 恒成立,则
恒成立,则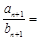 ( )
( )
A.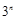 | B.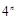 | C.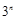 或 或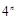 | D.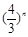 |
在等比数列 中,
中,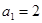 ,前
,前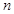 项和为
项和为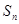 ,若数列
,若数列 也是等比数列,则
也是等比数列,则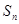 等于( )
等于( )
A. | B.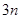 | C. | D. |
各项都是正数的等比数列{an}的公比q≠1且a2,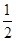 a3,a1成等差数列,则
a3,a1成等差数列,则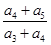 =( )
=( )
A.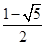 | B.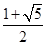 |
C.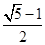 | D.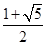 或 或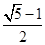 |
已知各项为正的等比数列{an}中,a4与a14的等比中项为 ,则2a7+a11的最小值为( )
,则2a7+a11的最小值为( )
| A.16 | B.8 | C. | D.4 |
 是正数组成的数列,
是正数组成的数列, ,且点
,且点 在函数
在函数 的图象上.数列
的图象上.数列 满足
满足 ,
, .
.
 ,求数列
,求数列 的前
的前 项和
项和 .
. ﹜满足:
﹜满足: .(Ⅰ)求数列﹛
.(Ⅰ)求数列﹛ ,求
,求