Question

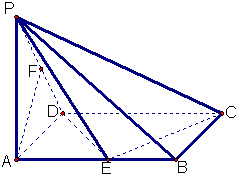
在四棱锥P－ABCD中，△PBC为正三角形，AB⊥平面PBC，AB∥CD，AB＝DC，E为PD中点．

(1)求证：AE∥平面PBC；

(2)求证：AE⊥平面PDC．

Answer 1

答案：
解析：

　　(1)证明：取PC的中点M，连接EM，

　　则EM∥CD，EM＝DC，所以有EM∥AB且EM＝AB，

　　则四边形ABME是平行四边形．所以AE∥BM，因为AE不在平面PBC内，所以AE∥平面PBC．

　　(2)因为AB⊥平面PBC，AB∥CD，所以CD⊥平面PBC，

　　CD⊥BM．由(1)得，BM⊥PC，所以BM⊥平面PDC，又AE∥BM，所以AE⊥平面PDC