题目内容
已知数列{an}满足a1=4,an=4 ,令
,令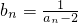 .
.
(1)求证数列{bn}是等差数列.(2)求数列{an}的通项公式.
解:(1) ,
,
 =
= ,
,
于是有 =
= +
+ ,
,
 ,即bn-bn-1=
,即bn-bn-1= ,
,
故有数列{bn}为等差数列,公差为 .
.
(2) =
= .
.
所以有bn= ,
,
于是有 ,
,
∴an= +2.
+2.
分析:(1)由题设知 ,于是有
,于是有 =
= +
+ ,bn-bn-1=
,bn-bn-1= ,由此可知数列{bn}为等差数列.
,由此可知数列{bn}为等差数列.
(2)由题设知bn= ,于是有
,于是有 ,两边同时取倒数后能够得到an=
,两边同时取倒数后能够得到an= +2.
+2.
点评:本题考查数列的性质和应用,解题时要注意等差数列的性质的应用和判断.
 ,
, =
= ,
,于是有
 =
= +
+ ,
, ,即bn-bn-1=
,即bn-bn-1= ,
,故有数列{bn}为等差数列,公差为
 .
.(2)
 =
= .
.所以有bn=
 ,
,于是有
 ,
,∴an=
 +2.
+2.分析:(1)由题设知
 ,于是有
,于是有 =
= +
+ ,bn-bn-1=
,bn-bn-1= ,由此可知数列{bn}为等差数列.
,由此可知数列{bn}为等差数列.(2)由题设知bn=
 ,于是有
,于是有 ,两边同时取倒数后能够得到an=
,两边同时取倒数后能够得到an= +2.
+2.点评:本题考查数列的性质和应用,解题时要注意等差数列的性质的应用和判断.

练习册系列答案
相关题目