题目内容
2.求证:1+$\frac{1}{{2}^{2}}$+$\frac{1}{{3}^{2}}$+…+$\frac{1}{{n}^{2}}$<2.分析 1+$\frac{1}{{2}^{2}}$+$\frac{1}{{3}^{2}}$+…+$\frac{1}{{n}^{2}}$<1+$\frac{1}{1×2}$+$\frac{1}{2×3}$+…+$\frac{1}{(n-1)n}$,再裂项,即可证明结论.
解答 证明:∵1+$\frac{1}{{2}^{2}}$+$\frac{1}{{3}^{2}}$+…+$\frac{1}{{n}^{2}}$<1+$\frac{1}{1×2}$+$\frac{1}{2×3}$+…+$\frac{1}{(n-1)n}$
=1+1-$\frac{1}{2}$+$\frac{1}{2}-\frac{1}{3}$+…+$\frac{1}{n-1}$-$\frac{1}{n}$=2-$\frac{1}{n}$<2,
∴1+$\frac{1}{{2}^{2}}$+$\frac{1}{{3}^{2}}$+…+$\frac{1}{{n}^{2}}$<2.
点评 本题考查用放缩法证明不等式,掌握好放缩的程度,是解题的难点.

练习册系列答案
相关题目
12. 如图,在棱长为1正四面体S-ABC,O是四面体的中心,平面PQR∥平面ABC,设SP=x(0≤x≤1),三棱锥O-PQR的体积为V=f(x),其导函数y=f(x)的图象大致为( )
如图,在棱长为1正四面体S-ABC,O是四面体的中心,平面PQR∥平面ABC,设SP=x(0≤x≤1),三棱锥O-PQR的体积为V=f(x),其导函数y=f(x)的图象大致为( )
 如图,在棱长为1正四面体S-ABC,O是四面体的中心,平面PQR∥平面ABC,设SP=x(0≤x≤1),三棱锥O-PQR的体积为V=f(x),其导函数y=f(x)的图象大致为( )
如图,在棱长为1正四面体S-ABC,O是四面体的中心,平面PQR∥平面ABC,设SP=x(0≤x≤1),三棱锥O-PQR的体积为V=f(x),其导函数y=f(x)的图象大致为( )| A. | 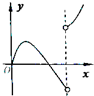 | B. |  | C. |  | D. |  |
12.在极坐标系中,曲线ρ=2cosθ是( )
| A. | 过极点的直线 | B. | 半径为2 的圆 | ||
| C. | 关于极点对称的图形 | D. | 关于极轴对称的图形 |
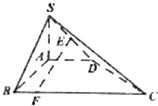 在四棱锥S-ABCD中,SA⊥平面ABCD,∠BAD=∠ABC=90°,SA=AB=AD=$\frac{1}{3}$BC=1,E为SD的中点.
在四棱锥S-ABCD中,SA⊥平面ABCD,∠BAD=∠ABC=90°,SA=AB=AD=$\frac{1}{3}$BC=1,E为SD的中点.