题目内容
已知函数 为
为 上的奇函数,且
上的奇函数,且 ,对任意
,对任意 ,有
,有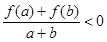 。 (1)判断函数
。 (1)判断函数 在
在 上的单调性,并证明你的结论;
上的单调性,并证明你的结论;
(2)解关于 的不等式
的不等式
【答案】
(1) 在
在 上的单调递减
上的单调递减
(2)当 时,不等式的解集为
时,不等式的解集为 ;
;
当 时,不等式的解集为
时,不等式的解集为 ;
;
当 时,原不等式变为:
时,原不等式变为:  ,
,
不等式的解集为
【解析】解:(1)由函数 为
为 上的奇函数,得
上的奇函数,得 ,又已知
,又已知 ,
,
所以函数 在
在 上的单调递减。
上的单调递减。
证明:令任意 ,在已知中,取
,在已知中,取 ,则
,则 ,
,
∵函数 为
为 上的奇函数,∴
上的奇函数,∴ ,又
,又 ,
,
∴ ,即
,即 。
。
∴函数 在
在 上的单调递减。……………………………………6分
上的单调递减。……………………………………6分
(2)∵ ∴由
∴由 得:
得:
∵函数 在
在 上的单调递减。 ∴
上的单调递减。 ∴ 即:
即:
∴当 时,不等式的解集为
时,不等式的解集为 ;
;
当 时,不等式的解集为
时,不等式的解集为 ;
;
当 时,原不等式变为:
时,原不等式变为:  ,
,
不等式的解集为 ……………………12分
……………………12分

练习册系列答案
相关题目
 为
为 上的奇函数,当
上的奇函数,当 时,
时, ,则当
,则当 时,
时, ___________.
___________. 为
为 上的奇函数,当
上的奇函数,当 时,
时, .若
.若 ,则实数
,则实数 .
. 为
为 上的奇函数,当
上的奇函数,当 时,
时, ,则当
,则当 时,
时, .
. 为
为 上的奇函数,当
上的奇函数,当 时,
时, .若
.若 ,则实数
,则实数 .
.