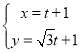题目内容
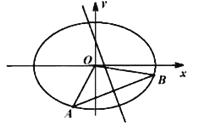
【题目】已知椭圆![]() 的左、右顶点分别为
的左、右顶点分别为![]() ,
,![]() ,左、右焦点分别为
,左、右焦点分别为![]() ,
,![]() ,离心率为
,离心率为![]() ,点
,点![]() ,
,![]() 为线段
为线段![]() 的中点.
的中点.

(![]() )求椭圆
)求椭圆![]() 的方程.
的方程.
(![]() )若过点
)若过点![]() 且斜率不为
且斜率不为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 、
、![]() 两点,已知直线
两点,已知直线![]() 与
与![]() 相交于点
相交于点![]() ,试判断点
,试判断点![]() 是否在定直线上?若是,请求出定直线的方程;若不是,请说明理由.
是否在定直线上?若是,请求出定直线的方程;若不是,请说明理由.
【答案】(1)![]() ;(2)点
;(2)点![]() 在定直线
在定直线![]() 上.
上.
【解析】
试题分析: (Ⅰ)求椭圆标准方程,一般方法为待定系数法,即根据条件建立关于![]() 的两个独立条件,再与
的两个独立条件,再与![]() 联立方程组,解出
联立方程组,解出![]() 的值,(Ⅱ)先根据特殊直线或椭圆几何性质确定定直线
的值,(Ⅱ)先根据特殊直线或椭圆几何性质确定定直线![]() ,再根据条件证明点
,再根据条件证明点![]() 横坐标为1.由题意设
横坐标为1.由题意设![]() 两点坐标,用
两点坐标,用![]() 两点坐标表示点
两点坐标表示点![]() 横坐标.根据直线
横坐标.根据直线![]() 方程与椭圆方程联立方程组,利用韦达定理得
方程与椭圆方程联立方程组,利用韦达定理得![]() 两点坐标关系(用直线
两点坐标关系(用直线![]() 斜率表示),并代入点
斜率表示),并代入点![]() 横坐标表达式,化简可得为定值.
横坐标表达式,化简可得为定值.
试题解析: (Ⅰ)设点![]() ,由题意可知:
,由题意可知:![]() ,即
,即![]() ①
①
又因为椭圆的离心率![]() ,即
,即![]() ②
②
联立方程①②可得:![]() ,则
,则![]()
所以椭圆![]() 的方程为
的方程为![]() .
.
(Ⅱ)方法一:根据椭圆的对称性猜测点![]() 是与
是与![]() 轴平行的直线
轴平行的直线![]() 上.
上.
假设当点![]() 为椭圆的上顶点时,直线
为椭圆的上顶点时,直线![]() 的方程为
的方程为![]() ,此时点
,此时点![]()
![]() ,
,
则联立直线![]() 和直线
和直线![]() 可得点
可得点![]()
据此猜想点![]() 在直线
在直线![]() 上,下面对猜想给予证明:
上,下面对猜想给予证明:
设![]() ,联立方程
,联立方程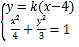 可得:
可得:![]()
由韦达定理可得![]() ,
,![]() (*)
(*)
因为直线![]() ,
,![]() ,
,
联立两直线方程得![]() (其中
(其中![]() 为
为![]() 点的横坐标)即证:
点的横坐标)即证:![]() ,
,
即![]() ,即证
,即证![]()
将(*)代入上式可得![]()
此式明显成立,原命题得证.所以点![]() 在定直线上
在定直线上![]() 上.
上.
方法二:设![]() ,
,![]() 两两不等,
两两不等,
因为![]() 三点共线,所以
三点共线,所以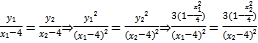 ,
,
整理得:![]()
又![]() 三点共线,有:
三点共线,有:![]() ①
①
又![]() 三点共线,有:
三点共线,有:![]() ② 将①与②两式相除得:
② 将①与②两式相除得:
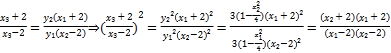
即![]() ,
,
将![]() 即
即![]() 代入得:
代入得:![]()
解得![]() (舍去)或
(舍去)或![]() ,所以点
,所以点![]() 在定直线
在定直线![]() 上.
上.
方法三:显然![]() 与
与![]() 轴不垂直,设
轴不垂直,设![]() 的方程为
的方程为![]() ,
,![]() .
.
由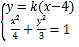 得
得![]() .
.
设![]() ,
,![]() 两两不等,
两两不等,
则![]() ,
,![]() ,
,![]()
由![]() 三点共线,有:
三点共线,有:![]() ①
①
由![]() 三点共线,有:
三点共线,有:![]() ②
②
①与②两式相除得:
![]()
解得![]() (舍去)或
(舍去)或![]() ,所以点
,所以点![]() 在定直线
在定直线![]() 上.
上.

练习册系列答案
相关题目