题目内容
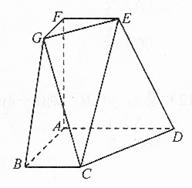
如图,直四棱柱ABCD-A1B1C1D1的底面ABCD为平行四边形,其中AB=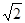 , BD=BC=1, AA1=2,E为DC的中点,F是棱DD1上的动点.
, BD=BC=1, AA1=2,E为DC的中点,F是棱DD1上的动点.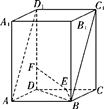
(1)求异面直线AD1与BE所成角的正切值;
(2)当DF为何值时,EF与BC1所成的角为90°?
(1)3;(2)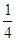
解析试题分析:(1)求异面直线所成的角,应该先找后求,异面直线所成的角是指将两条异面直线经过平行移动后,移到相交位置时,所成的锐角或直角,故平移直线是找异面直线所成角的关键,通常平移办法有中位线平移、平行四边形平移、比例线段平移,找到所求的角后,然后借助平面图形去求;(2)直线和直线 垂直,通常采取的办法是,先证明线面垂直,进而证明线线 垂直,而证明线面垂直,又需要两个线线垂直关系,所以需从图里尽可能挖掘隐藏的垂直关系.
试题解析:(1)连接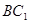 1.在直四棱柱ABCD-A1B1C1D1中,∵
1.在直四棱柱ABCD-A1B1C1D1中,∵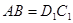 ,
,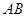 ∥
∥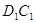 ,∴四边形
,∴四边形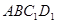 是平行四边形,所以
是平行四边形,所以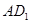 ∥
∥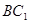 ,∴
,∴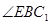 就是异面直线AD1与BE所成角或者是其补角,因为
就是异面直线AD1与BE所成角或者是其补角,因为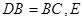 是边
是边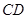 的中点,所以
的中点,所以 ,又在直四棱柱ABCD-A1B1C1D1中,
,又在直四棱柱ABCD-A1B1C1D1中,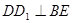 ,∴
,∴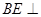 面
面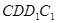 ,所以
,所以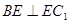 ,在Rt△BEC1中,BE=
,在Rt△BEC1中,BE=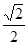 ,EC1=
,EC1=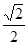 ,所以tan ∠EBC1=
,所以tan ∠EBC1= =3;
=3;
(2)当DF=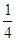 时,EF与BC1所成的角为9 0°,由(1)知,
时,EF与BC1所成的角为9 0°,由(1)知,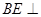 面
面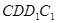 ,∴
,∴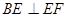 ,∴当
,∴当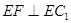 时,
时,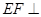 面
面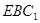 ,从而
,从而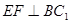 ,在矩形
,在矩形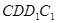 中,又DE=EC=
中,又DE=EC=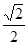 ,CC1=AA1=2.
,CC1=AA1=2.
当DF=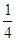 时,因为
时,因为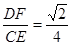 ,
,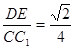 , 所以△DEF∽△CC1E,所以∠DEF+∠CEC1=90°,
, 所以△DEF∽△CC1E,所以∠DEF+∠CEC1=90°,
所以∠FEC1=90°,即FE⊥EC1.又EB∩EC1=E,所以EF⊥平面BEC1,
所以EF⊥BC1,即EF与BC1所成的角等于90°.
考点:1、异面直线所成的角;2、直线和平面垂直.

练习册系列答案
相关题目
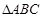 与
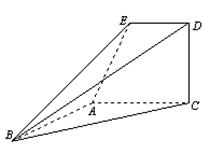
与 所在平面互相垂直,且
所在平面互相垂直,且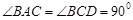 ,
,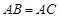 ,
,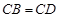 ,点
,点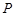 ,
, 分别在线段
分别在线段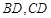 上,沿直线
上,沿直线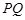 将
将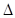
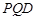 向上翻折,使
向上翻折,使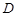 与
与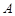 重合.
重合.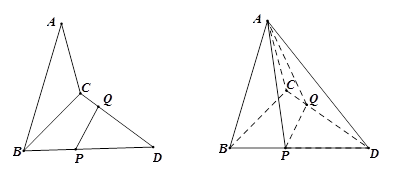
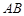
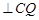 ;
;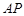 与平面
与平面 所成的角的正弦值.
所成的角的正弦值. 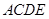 所在的平面垂直于平面
所在的平面垂直于平面 ,
,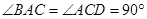 ,
,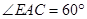 ,
,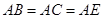 .
.
 是直线
是直线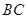 中点,证明
中点,证明 平面
平面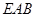 ;
;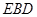 与平面
与平面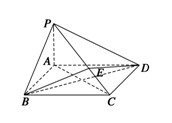
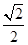 时,求四棱锥P-ABCD的外接球表面积.
时,求四棱锥P-ABCD的外接球表面积. 中,
中,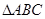 是正三角形,四边形
是正三角形,四边形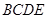 是矩形,且平面
是矩形,且平面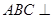 平面
平面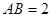 ,
,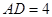 .
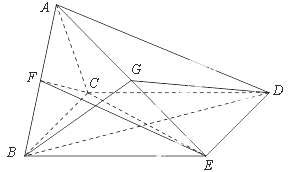
.
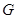 是
是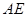 的中点,求证:
的中点,求证: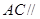 平面
平面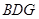 ;
;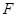 在线段
在线段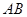 上什么位置时,二面角
上什么位置时,二面角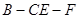 的余弦值为
的余弦值为 .
.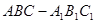 的侧面
的侧面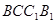 是菱形,
是菱形,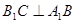 ,D是
,D是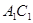 的中点,证明:
的中点,证明: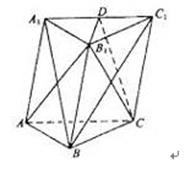
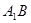 ∥面
∥面
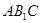
 平面
平面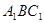 .
.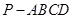 中,四边形
中,四边形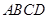 为矩形,
为矩形,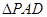 为等腰三角形,
为等腰三角形,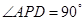 ,平面
,平面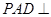 平面
平面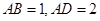 ,
,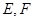 分别为
分别为 和
和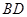 的中点.
的中点.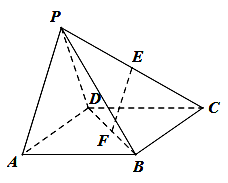
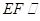 平面
平面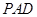 ;
;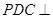 平面
平面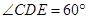 ,M是DE的中点,F是AC的中点,且AC=4,
,M是DE的中点,F是AC的中点,且AC=4,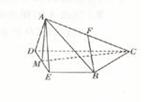
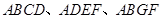 均为全等的直角梯形,且
均为全等的直角梯形,且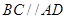 ,
,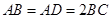 .
.
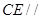 平面
平面 ;
;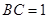 ,求点
,求点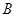 到平面
到平面 的距离.
的距离.