题目内容
 如图,圆O和圆O'相交于A,B两点,AC是圆O'的切线,AD是圆O的切线,若BC=2,AB=4,则BD=
如图,圆O和圆O'相交于A,B两点,AC是圆O'的切线,AD是圆O的切线,若BC=2,AB=4,则BD=分析:由AC是圆O'的切线,AD是圆O的切线,利用圆的弦切角等于所夹弧所对的圆周角,得到三角形ABC与三角形ABD相似,由相似得到三角形的对应边成比例得到一个关系式,把BC和AB的值代入关系式即可求出BD的值.
解答:解:因为AC是圆O′的切线,
∴∠CAB=∠D,
∵AD是圆O的切线,
∴∠BAD=∠C,
∴△ABC∽△DBA,
∴
=
,又BC=2,AB=4,
∴BD=
=8
故答案为:8
∴∠CAB=∠D,
∵AD是圆O的切线,
∴∠BAD=∠C,
∴△ABC∽△DBA,
∴
| AB |
| BC |
| BD |
| AB |
∴BD=
| AB2 |
| BC |
故答案为:8
点评:此题考查学生灵活运用弦切角定理以及三角形相似对应边成比例化简求值,是一道中档题.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
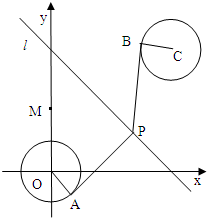 已知圆O:x2+y2=1,圆C:(x-4)2+(y-4)2=1,由两圆外一点P(a,b)引两圆切线PA、PB,切点分别为A、B,如图,满足|PA|=|PB|;
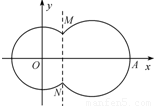
已知圆O:x2+y2=1,圆C:(x-4)2+(y-4)2=1,由两圆外一点P(a,b)引两圆切线PA、PB,切点分别为A、B,如图,满足|PA|=|PB|; (2011•盐城二模)如图,在平面直角坐标系xOy中,已知曲线C由圆弧C1和圆弧C2相接而成.两相接点M,N均在直线x=5上,圆弧C1的圆心是坐标原点O,半径为r1=13; 圆弧C2过点A(29,0).
(2011•盐城二模)如图,在平面直角坐标系xOy中,已知曲线C由圆弧C1和圆弧C2相接而成.两相接点M,N均在直线x=5上,圆弧C1的圆心是坐标原点O,半径为r1=13; 圆弧C2过点A(29,0). (Ⅲ)给出定点M(0,2),设P、Q分别为直线l和圆O上动点,求|MP|+|PQ|的最小值及此时点P的坐标.
(Ⅲ)给出定点M(0,2),设P、Q分别为直线l和圆O上动点,求|MP|+|PQ|的最小值及此时点P的坐标. PO?若存在,指出有几个这样的点;若不存在,请说明理由;
PO?若存在,指出有几个这样的点;若不存在,请说明理由;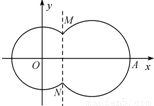
 PO?若存在,指出有几个这样的点;若不存在,请说明理由;
PO?若存在,指出有几个这样的点;若不存在,请说明理由;