题目内容
下列结论正确的是
- A.当x＞0且x≠1时，lgx+
- B.当x≥2时，
的最小值为2 - C.当0＜x≤2时，
无最大值 - D.当x＞0时，
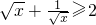
D
分析：对于A，在（0，1）上取一个数进行判定即可，对于B，最小值2时x=1，取不到；对于C，根据函数在（0，2]上单调增，可知x-
有最大值，选项D，直接利用基本不等式可证得结论，注意等号成立的条件．
解答：对于A，当0＜x＜1时，lgx＜0，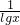
＜0，结论不成立；
对于B，x+在[2，+∞）上单调增，所以x=2时，x+的最小值为2
，故B错误；
对于C，x-在（0，2]上单调增，所以x=2时，x-取得最大值，故C不成立；
对于D，当x＞0时，
+
≥2，当且仅当x=1时，等号成立，故D成立
故选D．
点评：本题考查的重点是基本不等式的运用，解题的关键是明确基本不等式的使用条件，属于基础题．
分析：对于A，在（0，1）上取一个数进行判定即可，对于B，最小值2时x=1，取不到；对于C，根据函数在（0，2]上单调增，可知x-
有最大值，选项D，直接利用基本不等式可证得结论，注意等号成立的条件．解答：对于A，当0＜x＜1时，lgx＜0，
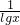＜0，结论不成立；对于B，x+
在[2，+∞）上单调增，所以x=2时，x+的最小值为2，故B错误；对于C，x-
在（0，2]上单调增，所以x=2时，x-取得最大值，故C不成立；对于D，当x＞0时，
+≥2，当且仅当x=1时，等号成立，故D成立故选D．
点评：本题考查的重点是基本不等式的运用，解题的关键是明确基本不等式的使用条件，属于基础题．
练习册系列答案
相关题目
则下列结论正确的是( )
)=
B.P(ξ≥
)=
)=
D.P(ξ≤
)=P(ξ≥
)
且
则下列结论正确的是
B.
C. 
D. 
为“三件产品全不是次品”，
为“三件产品全是次品”，
为“三件产品不全是次品”，则下列结论正确的是:
：
，
，那么下列结论正确的是( )
，
B．
，
D．