Question

已知A（2，1），B（3，2），D（-1，4）.

（1）求证：⊥；

（2）若四边形ABCD是矩形，试确定点C的坐标并求该矩形的两对角线所成的锐角的余弦值.

Answer 1

思路分析：本题主要考查向量垂直的等价条件及夹角公式.要证明⊥，只需证·=0.在⊥的前提下，只要找点C使=.

(1)证明：∵A(2,1),B(3,2),D(-1,4),

∴=(1,1),=(-3,3),

又·=1×(-3)+1×3=0,

∴⊥.

(2)解：∵四边形ABCD为矩形且AB⊥AD，

∴=.

设点C的坐标为（x,y）,

则（-3，3）=（x-3,y-2）,

∴∴

∴点C坐标为（0,5）.

又∵=（-2，4），=（-4，2），

∴·=（-2）×(-4)+4×2=16,

而||=，

||=.

设与的夹角为θ，则

cosθ=.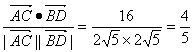

∴该矩形两对角线所成锐角的余弦值为.

温馨提示

(1)注意区分两向量平行与垂直的条件.

(2)向量的运算可以用坐标表示，向量中的位置关系（平行和垂直）也可用坐标表示，向量中的度量（模长和夹角）也可用坐标表示，而且使用起来非常方便，所以同学们要熟练掌握利用坐标法解决有关问题.