题目内容
函数y=sin（2x+
）图象的对称中心的坐标是________．
（
，0），k∈Z
分析：根据正弦函数图象与性质，令原题中三角函数中的角度等于kπ，解出x，即为对称中心的横坐标，又纵坐标为0，从而得到对称中心坐标．
解答：令2x+=kπ，k∈Z，
解得：x=
kπ-
，k∈Z，
则函数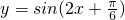
的图象的对称中心的坐标是（
，0）k∈Z．
故答案为：（，0）k∈Z
点评：此题考查了正弦函数的对称性，熟练掌握正弦函数的对称中心是解本题的关键．
，0），k∈Z分析：根据正弦函数图象与性质，令原题中三角函数中的角度等于kπ，解出x，即为对称中心的横坐标，又纵坐标为0，从而得到对称中心坐标．
解答：令2x+
=kπ，k∈Z，解得：x=
kπ-，k∈Z，则函数
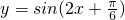的图象的对称中心的坐标是（，0）k∈Z．故答案为：（
，0）k∈Z点评：此题考查了正弦函数的对称性，熟练掌握正弦函数的对称中心是解本题的关键．
练习册系列答案
相关题目