题目内容
已知圆C:(x-1)2+(y-2)2=25,直线L:(2m+1)x+(m+1)y-7m-4=0(m∈R)(1)证明:无论m取什么实数,L与圆恒交于两点;
(2)求直线被圆C截得的弦长最小时直线L的斜截式方程.
【答案】分析:(1)将直线l方程整理后,确定出恒过的定点A坐标,判断A在圆C内部,即可确定出无论m取什么实数,L与圆恒交于两点;
(2)当直线被圆C截得的弦长最小时,直线l与直线AM垂直,根据直线AM的斜率求出l的斜率,再由A的坐标即可确定出直线l方程.
解答:解:(1)将直线l方程整理得:(x+y-4)+m(2x+y-7)=0,
由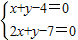 ,解得:
,解得: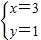 ,
,
∴直线l恒过A(3,1),
∵(3-1)2+(1-2)2=5<25,
∴点A在圆C内部,
则直线l与圆恒有两个交点;
(2)由圆的方程得到圆心M(1,2),当截得的弦长最小时,直线l⊥AM,
∵kAM=- ,∴直线l斜率为2,
,∴直线l斜率为2,
则直线l的方程为y-1=2(x-2),即2x-y-5=0.
点评:此题考查了直线与圆相交的性质,以及恒过定点的直线方程,根据题意得出截得的弦长最小时,直线l⊥AM是解本题第二问的关键.
(2)当直线被圆C截得的弦长最小时,直线l与直线AM垂直,根据直线AM的斜率求出l的斜率,再由A的坐标即可确定出直线l方程.
解答:解:(1)将直线l方程整理得:(x+y-4)+m(2x+y-7)=0,
由
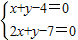 ,解得:
,解得: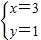 ,
,∴直线l恒过A(3,1),
∵(3-1)2+(1-2)2=5<25,
∴点A在圆C内部,
则直线l与圆恒有两个交点;
(2)由圆的方程得到圆心M(1,2),当截得的弦长最小时,直线l⊥AM,
∵kAM=-
 ,∴直线l斜率为2,
,∴直线l斜率为2,则直线l的方程为y-1=2(x-2),即2x-y-5=0.
点评:此题考查了直线与圆相交的性质,以及恒过定点的直线方程,根据题意得出截得的弦长最小时,直线l⊥AM是解本题第二问的关键.

练习册系列答案
相关题目