题目内容
甲:函数f(x)是奇函数;乙:函数f(x)在定义域上是增函数.对于函数①f(x)=-| 1 |
| x |
|
分析:本题考查的知识点是函数的性质,根据函数f(x)是奇函数及函数f(x)在定义域上是增函数逐一分析四个条件,不难得到答案.
解答:解:①f(x)=-
,在其定义域上不是增函数,故①不正确;
②f(x)=tan x,在其定义域上不是增函数,故②不正确;
③④即是奇函数,又在定义域上为增函数,符合条件,故③④正确.
故答案为:③④
| 1 |
| x |
②f(x)=tan x,在其定义域上不是增函数,故②不正确;
③④即是奇函数,又在定义域上为增函数,符合条件,故③④正确.
故答案为:③④
点评:本题综合的考查了多个函数的性质,解决本题的关键是熟练掌握各个函数的性质,然后逐一对照条件,判断条件是否满足,即可得到答案.

练习册系列答案
相关题目
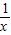 ,
,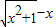 ),
), ,
,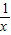 ,
,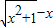 ),
),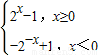 ,
, ,②f(x)=tan x,③f(x)=x|x|,④
,②f(x)=tan x,③f(x)=x|x|,④ 能使甲,乙均为真命题的所有函数的序号是 .
能使甲,乙均为真命题的所有函数的序号是 .