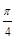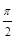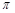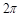题目内容
(本小题满分12分) 锐角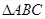 中,角A、B、C所对的边分别为
中,角A、B、C所对的边分别为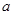 、
、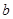 、
、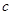 ,且
,且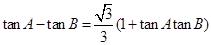 .
.
(1)若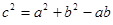 ,求角A、B、C大小;
,求角A、B、C大小;
(2)已知向量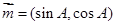 ,
,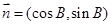 ,求
,求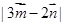 的取值范围.
的取值范围.
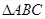 中,角A、B、C所对的边分别为
中,角A、B、C所对的边分别为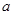 、
、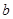 、
、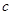 ,且
,且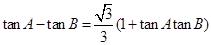 .
.(1)若
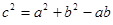 ,求角A、B、C大小;
,求角A、B、C大小;(2)已知向量
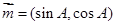 ,
,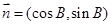 ,求
,求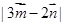 的取值范围.
的取值范围. (1)  ,
, ,
, ;(2)
;(2) 
 。
。
 ,
, ,
, ;(2)
;(2) 
 。
。本试题主要是考查了三角函数的化简和向量的数量积的运用。
(1)由已知得:
又 从而
从而 即
即 结合余弦定理
结合余弦定理 得到角C的值。
得到角C的值。
(2)要求向量 模长可以先平方,借助于向量的数量积得到。
解:(1)由已知得:
又 从而
从而 即
即 …………2分
…………2分
由 ,得
,得 ,可得
,可得
又因为 ,
, ,
,
可得: ,
, ,
, …………6分
…………6分
2)
…………8分
由

得
从而 故
故
即
 …………12分
…………12分
(1)由已知得:

又
 从而
从而 即
即 结合余弦定理
结合余弦定理 得到角C的值。
得到角C的值。(2)要求向量 模长可以先平方,借助于向量的数量积得到。
解:(1)由已知得:

又
 从而
从而 即
即 …………2分
…………2分由
 ,得
,得 ,可得
,可得
又因为
 ,
, ,
,可得:
 ,
, ,
, …………6分
…………6分2)

…………8分
由


得

从而
 故
故
即

 …………12分
…………12分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,
,
 的图像.
的图像. 的图象是由
的图象是由 的图象经过怎样的变换得到的.
的图象经过怎样的变换得到的.
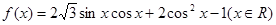 。
。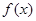 的最小正周期及在区间
的最小正周期及在区间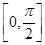 上的最大值和最小值;
上的最大值和最小值;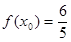 ,
,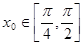 ,求
,求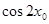 的值。
的值。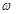 x在[-
x在[-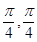 ]上单调递增,则正实数
]上单调递增,则正实数 的图象,只需将函数
的图象,只需将函数 的图象( )
的图象( ) 向右平移
向右平移 个单位
个单位  向左平移
向左平移 向右平移
向右平移 个单位
个单位  向左平移
向左平移 .
. ,求
,求 的值;
的值; 的单调增区间.
的单调增区间. .
. 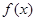 的最小正周期和当
的最小正周期和当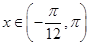 时的值域;
时的值域; 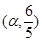 ,
,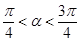 .求
.求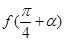 的值.
的值. ,且
,且 =
= 则( )
则( ) ≤
≤ ≤
≤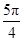

 ≤
≤
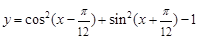 的最小正周期为( ).
的最小正周期为( ).