题目内容
若函数
的定义域为R，则m的取值范围是 ．
【答案】分析：函数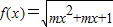
的定义域为R，可得mx2+mx+1≥0恒成立分m=0，m≠0两种情况讨论
解答：解：函数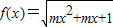
的定义域为R，
则mx2+mx+1≥0恒成立
当m=0时 1≥0恒成立
当m≠0时，则m＞0，m2-4m≤0⇒0＜m≤4
综上可得，0≤m≤4
故答案为：[0，4]
点评：本题以函数的定义域的考查为载体，考查了不等式的恒成立问题，体现了转化思想及分类讨论的思想的应用．
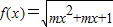的定义域为R，可得mx2+mx+1≥0恒成立分m=0，m≠0两种情况讨论解答：解：函数
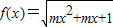的定义域为R，则mx2+mx+1≥0恒成立
当m=0时 1≥0恒成立
当m≠0时，则m＞0，m2-4m≤0⇒0＜m≤4
综上可得，0≤m≤4
故答案为：[0，4]
点评：本题以函数的定义域的考查为载体，考查了不等式的恒成立问题，体现了转化思想及分类讨论的思想的应用．
练习册系列答案
培优口算题卡系列答案
开心口算题卡系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
的定义域为R，则实数 的取值范围 （
）。
B、
C、
D、