题目内容
已知抛物线 与双曲线
与双曲线 有相同的焦点F,点A是两曲线的交点,且|AF|=p,则双曲线的离心率为( )
有相同的焦点F,点A是两曲线的交点,且|AF|=p,则双曲线的离心率为( )
A. +1 B.
+1 B. +l
+l
C. D.
D.
【答案】
A
【解析】
试题分析:由抛物线的定义可得A到抛物线的焦点F的距离为p,故AF垂直于x轴,把x= 代入y2=2px解得点A的坐标,再由椭圆的定义求得椭圆的离心率e=
代入y2=2px解得点A的坐标,再由椭圆的定义求得椭圆的离心率e= 的值解:由题可得图,设椭圆另一焦点为E,因为抛物线y2=2px(p>0)的焦点F(
的值解:由题可得图,设椭圆另一焦点为E,因为抛物线y2=2px(p>0)的焦点F( ,0).由抛物线的定义可得A到抛物线的焦点F的距离为p,故AF垂直于x轴.把x=
,0).由抛物线的定义可得A到抛物线的焦点F的距离为p,故AF垂直于x轴.把x= 代入y2=2px解得y=±p,所以A(
代入y2=2px解得y=±p,所以A( ,p),同时点F(-
,p),同时点F(- ,0),那么可知|AF|=p,由双曲线的定义可知AE=
,0),那么可知|AF|=p,由双曲线的定义可知AE= P,那么可知e=
P,那么可知e= +1,选A.
+1,选A.
考点:抛物线、双曲线的定义
点评:本题主要考查抛物线、双曲线的定义、标准方程,以及它们的简单性质的应用,在做圆锥曲线问题时,用定义来解题是比较常用的方法,属于中档题

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 与双曲线
与双曲线 有相同的焦点
有相同的焦点 ,点
,点 是两曲线的一个交点,且
是两曲线的一个交点,且 ⊥
⊥ 轴,则双曲线的离心率为
.
轴,则双曲线的离心率为
. 与双曲线
与双曲线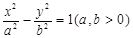 有相同的焦点
有相同的焦点 ,点
,点 是两曲线的一个交点,且
是两曲线的一个交点,且 轴,若
轴,若 为双曲线的一条斜率大于0的渐近线,则
为双曲线的一条斜率大于0的渐近线,则 (B)
(B) (C)
(C) (D)
(D)
 与双曲线
与双曲线 有相同的焦点
有相同的焦点 .点
.点 是两曲线的一个交点,
是两曲线的一个交点, 轴.若直线
轴.若直线 是双曲线的一条渐近线,则直线
是双曲线的一条渐近线,则直线 B.
B. C.
C. D.
D.
 与双曲线
与双曲线 有相同的焦点
有相同的焦点 ,点
,点 是两曲线的一个交点,
是两曲线的一个交点, 轴,若直线
轴,若直线 是双曲线的一条渐近线,则直线
是双曲线的一条渐近线,则直线 B.
B. C.
C. D.
D.