题目内容
一个几何体的三视图如图所示,则该几何体的体积(单位:cm3)为

- A.π+

- B.2

- C.2π

- D.

A
分析:由三视图可以看出,该几何体下部是一个圆柱,上部是一三棱锥,圆柱半径为1高也是1,三棱锥底面是一等腰直角三角形,过斜边的侧面与多方面垂直且该侧面是一等边三角形,边长是2,由于该几何体是一组合体故其体积为圆柱的体积与棱锥体积的和.
解答:由三视图,该组合体上部是一三棱锥,下部是一圆柱由图中数据知
V圆柱=π×12×1=π
三棱锥垂直于底面的侧面是边长为2的等边三角形,且边长是2,故其高即为三棱锥的高,高为
故棱锥高为
由于棱锥底面为一等腰直角三角形,且斜边长为2,故两直角边长度都是
底面三角形的面积是 =1
=1
故 =
=
故该几何体的体积是π+
故选A.
点评:本题考点是由三视图还原实物图,考查由在视图给出几何体的度量,由公式求体积,本题是三视图考查中常出现的题型,关键是正确地还原出几何体的特征.
分析:由三视图可以看出,该几何体下部是一个圆柱,上部是一三棱锥,圆柱半径为1高也是1,三棱锥底面是一等腰直角三角形,过斜边的侧面与多方面垂直且该侧面是一等边三角形,边长是2,由于该几何体是一组合体故其体积为圆柱的体积与棱锥体积的和.
解答:由三视图,该组合体上部是一三棱锥,下部是一圆柱由图中数据知
V圆柱=π×12×1=π
三棱锥垂直于底面的侧面是边长为2的等边三角形,且边长是2,故其高即为三棱锥的高,高为

故棱锥高为

由于棱锥底面为一等腰直角三角形,且斜边长为2,故两直角边长度都是

底面三角形的面积是
 =1
=1故
 =
=
故该几何体的体积是π+

故选A.
点评:本题考点是由三视图还原实物图,考查由在视图给出几何体的度量,由公式求体积,本题是三视图考查中常出现的题型,关键是正确地还原出几何体的特征.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
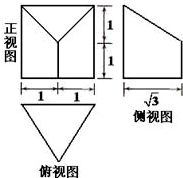
 (2013•房山区二模)一个几何体的三视图如图所示,则这个几何体的表面积为( )
(2013•房山区二模)一个几何体的三视图如图所示,则这个几何体的表面积为( )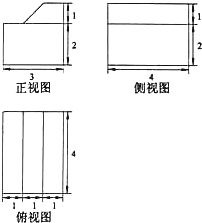 (2012•天津)一个几何体的三视图如图所示(单位:m),则该几何体的体积为
(2012•天津)一个几何体的三视图如图所示(单位:m),则该几何体的体积为 一个几何体的三视图如图所示,其中正视图是一个正三角形,则这个几何体的表面积为
一个几何体的三视图如图所示,其中正视图是一个正三角形,则这个几何体的表面积为 (2010•河东区一模)一个几何体的三视图如图所示,则该几何体(不考虑接触点)的表面积为
(2010•河东区一模)一个几何体的三视图如图所示,则该几何体(不考虑接触点)的表面积为