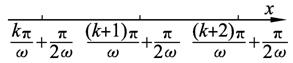Question

ω是正实数，设S_ω={θ|f（x）=cos[ω（x+θ）]是奇函数}，若对每个实数a，S_ω∩（a，a+1）的元素不超过2个，且有a使S_ω∩（a，a+1）含2个元素，则ω的取值范围是

 

．

Answer 1

分析：由S_ω={θ|f（x）=cos[ω（x+θ）]是奇函数}，推出S_ω的范围，S_ω∩（a，a+1）的元素不超过2个，且有a使S_ω∩（a，a+1）含2个元素，
推出

2

2ω

π＜1且2×

2

2ω

π≥1，求得ω的范围．

解答：解：S_ω={θ|f（x）=cos[ω（x+θ）]是奇函数}?S_ω={θ=

2k+1

2ω

π，k∈Z}={-

3

2ω

π，-

1

2ω

π，

1

2ω

π，

3

2ω

π}
因为对每个实数a，S_ω∩（a，a+1）的元素不超过2个，
且有a使S_ω∩（a，a+1）含2个元素，也就是说S_ω中任意相邻的两个元素之间隔必小于1，
并且S_ω中任意相邻的三个元素的两间隔之和必大于等于1，
即

2

2ω

π＜1且2×

2

2ω

π≥1；
解可得π＜ω≤2π．
故答案为：（π，2π]

点评：本题考查余弦函数的奇偶性，集合的包含关系判断及应用，考查计算推理能力，是中档题．