题目内容

P为椭圆+=1上的一点,F1和F2是其焦点,若∠F1PF2=60°,则△F1PF2的面积为__________________.

解：利用椭圆定义和三角形的面积公式.

∵|PF1|+|PF2|=2a=20,|F1F2|=2c=2=12,

由余弦定理得|F1F2|2=|PF1|2+|PF2|2-2|PF1||PF2|cos∠F1PF2=(|PF1|+|PF2|)2-2|PF1||PF2|-2|PF1||PF2|cos∠F1PF2.

故有122=202-2|PF1||PF2|-2|PF1||PF2|cos60°.

∴3|PF1||PF2|=400-144=256.

∴|PF1||PF2|=.

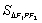∴Equation.3=|PF1||PF2|sin60°=××=.


练习册系列答案
相关题目
（2013•揭阳一模）如图，设点F1（-c，0）、F2（c，0）分别是椭圆C：
x2
a2
+y2=1(a＞1)的左、右焦点，P为椭圆C上任意一点，且
PF1
•
PF2
最小值为0．
（1）求椭圆C的方程；
（2）设直线l1：y=kx+m，l2：y=kx+n，若l1、l2均与椭圆C相切，证明：m+n=0；
（3）在（2）的条件下，试探究在x轴上是否存在定点B，点B到l1，l2的距离之积恒为1？若存在，请求出点B坐标；若不存在，请说明理由．
（2012•甘肃一模）设椭圆M：
x2
a2
+
y2
2
=1(a＞
2
)的右焦点为F1，直线l：x=
a2
a2-2
与x轴交于点A，若
OF1
+2
AF1
=0（其中O为坐标原点）．
（1）求椭圆M的方程；
（2）设P是椭圆M上的任意一点，EF为圆N：x2+（y-2）2=1的任意一条直径（E、F为直径的两个端点），求
PE
•
PF
的最大值．
（2013•温州一模）椭圆M：
x2
a2
+
y2
b2
=1(a＞b＞0)长轴上的两个顶点A、B，点P为椭圆M上除A、B外的一个动点，若
QA
•
PA
=0且
QB
•
PB
=0，则动点Q在下列哪种曲线上（　　）
（2012•青岛一模）已知点M在椭圆D：
x2
a2
+
y2
b2
=1（a＞b＞0）上，以M为圆心的圆与x轴相切于椭圆的右焦点，若圆M与y轴相交于A，B两点，且△ABM是边长为
2
6
3
的正三角形．
（Ⅰ）求椭圆D的方程；
（Ⅱ）设P是椭圆D上的一点，过点P的直线l交x轴于点F（-1，0），交y轴于点Q，若
QP
=2
PF
，求直线l的斜率；
（Ⅲ）过点G（0，-2）作直线GK与椭圆N：
3x2
a2
+
4y2
b2
=1左半部分交于H，K两点，又过椭圆N的右焦点F1做平行于HK的直线交椭圆N于R，S两点，试判断满足|GH|•|GK|=3|RF1|•|F1S|的直线GK是否存在？请说明理由．
已知P为椭圆+=1上一点,P到一条准线的距离为P到相应焦点的距离之比为(    )

A.               B.                C.               D.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网