题目内容
已知函数f（x）=Asin（ωx+φ），x∈R（其中A＞0，ω＞0，
），其部分图象如图所示．
（I）求f（x）的解析式；
（II）求函数
在区间
上的最大值及相应的x值．
解：（I）由图可知，A=1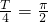 
，所以T=2π
所以ω=1
又
，且
所以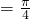
所以
．
（II）由（I），
所以=
=
=cosx•sinx
=
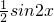
因为
，所以2x∈[0，π]，sin2x∈[0，1]
故：
，
当
时，g（x）取得最大值
．
分析：（I）先求周期，推出ω，利用（
），推出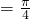，得到f（x）的解析式；
（II）求函数在区间上的最大值及相应的x值．
点评：本题考查由y=Asin（ωx+φ）的部分图象确定其解析式，三角函数的最值，考查学生视图能力，是基础题．
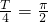，所以T=2π所以ω=1
又
，且所以
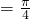
所以
．（II）由（I）
，所以
===cosx•sinx
=
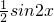
因为
，所以2x∈[0，π]，sin2x∈[0，1]故：
，当
时，g（x）取得最大值．分析：（I）先求周期，推出ω，利用（
），推出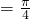，得到f（x）的解析式；（II）求函数
在区间上的最大值及相应的x值．点评：本题考查由y=Asin（ωx+φ）的部分图象确定其解析式，三角函数的最值，考查学生视图能力，是基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目