题目内容
在△ABC中,a、b、c分别是角A、B、C的对边, ,S△ABC=2.
,S△ABC=2.
(1)求 的值;
的值;
(2)设函数 ,最小正周期为π,当x等于角C时函数取到最大值,求使该函数取最小值时的x的集合.
,最小正周期为π,当x等于角C时函数取到最大值,求使该函数取最小值时的x的集合.
解:(1)根据余弦定理可得 ,
,
∵0<C<π,∴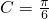
∵S△ABC=2,∴ ,∴ab=8
,∴ab=8
∴ ;
;
(2)函数当x= 时取最大值,当且仅当
时取最大值,当且仅当 ,即
,即
此时 .
.
 ,∴
,∴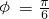 .
.
∴当 时取最小值.
时取最小值.
即 .
.
分析:(1)由 得出
得出 ,根据余弦定理及特殊角的三角函数值求出C的度数,再根据面积公式
,根据余弦定理及特殊角的三角函数值求出C的度数,再根据面积公式 absinC和已知面积等于2求出ab的值,然后根据平面向量的数量积的运算法则表示出
absinC和已知面积等于2求出ab的值,然后根据平面向量的数量积的运算法则表示出 ,把ab代入即可求出;
,把ab代入即可求出;
(2)由正弦函数的周期为π根据周期公式T=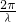 ,求出ω=2,再根据正弦函数求最值的方法得到
,求出ω=2,再根据正弦函数求最值的方法得到 ,把x=
,把x= 代入即可求出φ的范围,因为φ为锐角确定出φ的度数,所以将φ的度数代入得:当
代入即可求出φ的范围,因为φ为锐角确定出φ的度数,所以将φ的度数代入得:当 时取最小值,解出x即可.
时取最小值,解出x即可.
点评:考查学生灵活运用余弦定理及三角形的面积公式,会进行平面向量的数量积运算,会根据条件求正弦函数的最小值,会求正弦函数的周期,牢记特殊角的三角函数值.
 ,
,∵0<C<π,∴
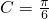
∵S△ABC=2,∴
 ,∴ab=8
,∴ab=8∴
 ;
;(2)函数当x=
 时取最大值,当且仅当
时取最大值,当且仅当 ,即
,即
此时
 .
. ,∴
,∴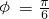 .
.∴当
 时取最小值.
时取最小值.即
 .
.分析:(1)由
 得出
得出 ,根据余弦定理及特殊角的三角函数值求出C的度数,再根据面积公式
,根据余弦定理及特殊角的三角函数值求出C的度数,再根据面积公式 absinC和已知面积等于2求出ab的值,然后根据平面向量的数量积的运算法则表示出
absinC和已知面积等于2求出ab的值,然后根据平面向量的数量积的运算法则表示出 ,把ab代入即可求出;
,把ab代入即可求出;(2)由正弦函数的周期为π根据周期公式T=
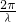 ,求出ω=2,再根据正弦函数求最值的方法得到
,求出ω=2,再根据正弦函数求最值的方法得到 ,把x=
,把x= 代入即可求出φ的范围,因为φ为锐角确定出φ的度数,所以将φ的度数代入得:当
代入即可求出φ的范围,因为φ为锐角确定出φ的度数,所以将φ的度数代入得:当 时取最小值,解出x即可.
时取最小值,解出x即可.点评:考查学生灵活运用余弦定理及三角形的面积公式,会进行平面向量的数量积运算,会根据条件求正弦函数的最小值,会求正弦函数的周期,牢记特殊角的三角函数值.

练习册系列答案
相关题目
在△ABC中,∠A、∠B、∠C所对的边长分别是a、b、c.满足2acosC+ccosA=b.则sinA+sinB的最大值是( )
A、
| ||||
| B、1 | ||||
C、
| ||||
D、
|