题目内容

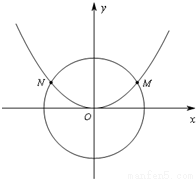
如图，已知抛物线C1：y=x2，与圆C­2：x2+（y+1）2=1，过y轴上一点A（0，a），（a>0）,作圆C2的切线AD,切点为D（x0，y0）.

（1）证明：（a+1）（y0+1）=1；

（2）若切线AD交抛物线C1于E，且E为AD的中点，求点A纵坐标a.

（1）证明：因为AD是圆的切线，所以AD⊥C­2­D，

于是有

即…………（1）

又因为…………（2）

由（2）－（1）得

即结论成立

（2）因为E为AD的中点，其坐标为，所以

即

又因为

即

也即

得（因为切线x轴，显然不符合题意，舍去）

或（不满足圆的条件，舍去）。

所以

再由

练习册系列答案
相关题目
（2013•嘉兴二模）如图，已知抛物线C1：x2=2py的焦点在抛物线C2：y=
12
x2+1上，点P是抛物线C1上的动点．
（Ⅰ）求抛物线C1的方程及其准线方程；
（Ⅱ）过点P作抛物线C2的两条切线，M、N分别为两个切点，设点P到直线MN的距离为d，求d的最小值．
（2013•嘉兴二模）如图，已知抛物线C1：x2=2py的焦点在抛物线C2：y=
12
x2+1上．
（Ⅰ）求抛物线C1的方程及其准线方程；
（Ⅱ）过抛物C1上的动点P作抛物线C2的两条切线PM、PN，切点M、N．若PM、PN的斜率积为m，且m∈[2，4]，求|OP|的取值范围．
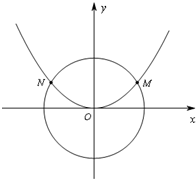精英家教网如图，已知抛物线C1：x2=2py（p＞0）与圆C2：x2+y2=
16
9
交于M、N两点，
且∠MON=120°．
（Ⅰ）求抛物线C1的方程；
（Ⅱ）设直线l与圆C2相切．
（ⅰ）若直线l与抛物线C1也相切，求直线l的方程；
（ⅱ）若直线l与抛物线C1交与不同的A、B两点，求
OA
•
OB
的取值范围．

（14分）如图，已知抛物线C1： y=x2, 与圆C2： x2+(y+1)2="1," 过y轴上一点A（0, a）（a>0）作圆C2的切线AD，切点为D（x0, y0）.

（1）证明：(a+1)(y0+1)=1

（2）若切线AD交抛物线C1于E，且E为AD的中点，求点A纵坐标a.

 
如图，已知抛物线C1：x2=2py（p＞0）与圆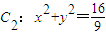交于M、N两点，
且∠MON=120°．
（Ⅰ）求抛物线C1的方程；
（Ⅱ）设直线l与圆C2相切．
（ⅰ）若直线l与抛物线C1也相切，求直线l的方程；
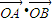（ⅱ）若直线l与抛物线C1交与不同的A、B两点，求的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网