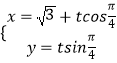题目内容
【题目】已知f（x）= 
，g（x）=ax3﹣x2﹣x+b（a，b∈R，a≠0），g（x）的图象C在x=﹣ 
处的切线方程是y= 
．
（1）若求a，b的值，并证明：当x∈（﹣∞，2]时，g（x）的图象C上任意一点都在切线y= 上或在其下方；
（2）求证：当x∈（﹣∞，2]时，f（x）≥g（x）．
【答案】
（1）解：g'（x）=3ax2﹣2x﹣1，
因为g（x）=ax3﹣x2﹣x+b的图象C在 
处的切线方程是 
，
所以 
，即 
，解得a=1．
因为图象C过点 
，所以 
，解得 
．
要证明：当x∈（﹣∞，2]时，g（x）的图象C上任意一点都在切线 上或在其下方，
只要证明：当x∈（﹣∞，2]时， 
．
令 
，
，令 
，得 
，
验证得 
，
所以x∈（﹣∞，2]， 成立，
所以当x∈（﹣∞，2]时，g（x）的图象C上任意一点都在切线 上或在其下方
（2）解：只要证明：x∈（﹣∞，2]， 
．
x∈（﹣∞，2]，令 
，
，令 
，
当 
时，h'（x）＜0，当 
时，h'（x）＞0，所以 
，
所以x∈（﹣∞，2]， 成立，
又由（1）得，x∈（﹣∞，2]， ，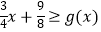
所以x∈（﹣∞，2]， 
，
所以x∈（﹣∞，2]，f（x）≥g（x）．
【解析】（1）求出函数的导数，根据 ，求出a的值，图象C过点 ，求出b的值，问题转化为证明当x∈（﹣∞，2]时， ，根据函数的单调性证明即可；（2）问题转化为证明x∈（﹣∞，2]， ，构造函数g（x），根据函数的单调性证明即可．
【考点精析】认真审题，首先需要了解函数的最大(小)值与导数(求函数
在
上的最大值与最小值的步骤：（1）求函数在
内的极值；（2）将函数的各极值与端点处的函数值
，
比较，其中最大的是一个最大值，最小的是最小值)．
