Question

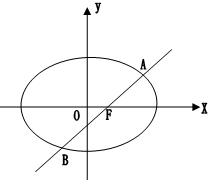已知椭圆

x2

a2

+

y2

a2

=1(a＞b＞0)的离心率为

2

2

，右焦点为F（1，0），直线l经过点F且与椭圆交于A、B两点，O为坐标原点．
（1）求椭圆的方程；
（2）若P是椭圆上的一个动点，求|PO|²+|PF|²的最大值和最小值；
（3）当直线l绕点F转动时，试问：在x轴上是否存在定点S，使

SA

•

SB

为常数，若存在，求出定点S的坐标；若不存在，请说明理由．

Answer 1

分析：（1）由椭圆的右焦点为F（1，0），可求c值，再根据离心率为

2

2

，可求出a的值，由a，b，c的关系得到b，则椭圆的方程就能求出．
（2）把|PO|²+|PF|²用P点坐标表示，再根据P点在椭圆上，横纵坐标有范围，就可得到|PO|²+|PF|²的最大值和最小值．
（3）因为直线l绕点F转动，可设出直线l的点斜式方程，与椭圆方程联立，设S点坐标，代入计算

SA

•

SB

，若计算结果为常数，则存在，否则，不存在．

解答：解：（1）e=

2

2

，c=1即

c

a

=

1

a

=

2

2

，a=

2

，b=1，所以椭圆方程

x2

2

+y2=1
（2）设P(x0，y0)，则

x 2 0

2

+

y

2 0

=1，
即2y₀²=2-x₀²，F（1，0）|PO|²+|PF|²=x₀²+y₀²+（x₀-1）²+y₀²=2y₀²+x₀²+（x₀-1）²=（x₀-1）²+2
而2y₀²=2-x₀²≥0，∴-

2

≤x0≤

2

当x₀=1时，（|PO|²+|PF|²）_min=2，当x0=-

2

时，(|PO|2+|PF|2)max=5+2

2

（3）①若直线l斜率存在时，设l方程为y=k（x-1）
由

y=k(x-1) x2+2y2=2

消去y得（1+2k²）x²-4k²x+2k²-2=0
设S（t，0）、A（x₁，y₁）、B（x₂，y₂）

SA • SB =(x1-t)(x2-t)+y1y2 =(x1-t)(x2-t)+k2(x1-1)(x2-1) =(1+k2)x1x2-(t+k2)(x1+x2)+t2+k2

=(1+k2)×

2k2-2

1+2k2

-(t+k2)×

4k2

1+2k2

+t2+k2=λ（λ为常数）
即2（k²+1）（k²-1）-4k²（t+k²）+（1+2k²）（t²+k²）=λ（1+2k²）（2t²-4t-2λ+1）k²+t²-λ-2=0
由

2t2-4t-2λ+1=0 t2-λ-2=0

，解得t=

5

4

，λ=-

7

16

②若斜率κ不存在时，A(1，

2

2

)、B(1，-

2

2

)、S（t，0）

SA

•

SB

=(1-t，

2

2

)•(1-t，-

2

2

)=(1-t)2-

1

2

=-

7

16

，t=

5

4

综上得，存在S(

5

4

，0)，使

SA

•

SB

=-

7

16

．

点评：本题考查了椭圆方程的求法，以及存在性问题的解法，属于常规题，应当掌握．