题目内容
对于函数f(x),若f(x)=x,则称x为f(x)的“不动点”;若f(f(x))=x,则称x为f(x)的“稳定点”.函数的“不动点”和“稳定点”的集合分别记为A和B,即A={x|f(x)=x},B={x|f(f(x))=x}.
(1)求证![]() ;
;
(2)若f(x)=ax2-1(a∈R,x∈R),且![]() ,求实数a的取值范围;
,求实数a的取值范围;
(3)若f(x)是R上的单调递增函数,x0是函数的稳定点,问x0是函数的不动点吗?若是,请证明你的结论;若不是,请说明理由.
答案:
解析:
解析:
|
解:(1)若 若 (2)因为 又 ∵A=B,∴方程 若方程 ∴a的取值范围是 (3)由题意 若 |

练习册系列答案
相关题目
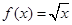 的等域区间是 .
的等域区间是 .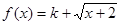 是布林函数,则实数k的取值范围是
.
是布林函数,则实数k的取值范围是
.