题目内容
已知f(x)是最小正周期为2的函数,当x∈(-1,1]时,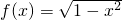 ,若在区间(3,5]上f(x)=ax有两个不相等的实数根,则实数a的取值范围是________.
,若在区间(3,5]上f(x)=ax有两个不相等的实数根,则实数a的取值范围是________.

分析:利用函数的周期是2,得到函数f(x)在区间(3,5]上的 表达式,然后利用直线与圆的位置关系进行判断.
解答:因为f(x)是最小正周期为2的函数,所以当x∈(3,5]时,x-4∈(-1,1],

所以f(x)=f(x-4)=
 ,即(x-4)2+y2=1,(y≥0),表示以(4,0)为圆心,半径为1的上半圆.
,即(x-4)2+y2=1,(y≥0),表示以(4,0)为圆心,半径为1的上半圆.当直线y=ax(a>0)与圆相切时,得圆心到直线ax-y=0的距离d=
 ,即
,即 ,解得
,解得 ,
,所以要使在区间(3,5]上f(x)=ax有两个不相等的实数根,则
 .
.故答案为:
 .
.点评:本题主要考查了函数周期性的应用,以及直线与圆的位置关系的应用,利用数形结合是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
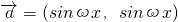 ,
,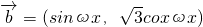 ,其中ω>0,设函数f(x)=2
,其中ω>0,设函数f(x)=2 ,已知f(x)的最小正周期为π.
,已知f(x)的最小正周期为π. 是g(x)图象的一条对称轴.
是g(x)图象的一条对称轴. ,
, ,其中ω>0,设函数f(x)=2
,其中ω>0,设函数f(x)=2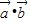 ,已知f(x)的最小正周期为π.
,已知f(x)的最小正周期为π. 是g(x)图象的一条对称轴.
是g(x)图象的一条对称轴.