题目内容
已知多面体ABCDE中，AB⊥平面ACD，DE⊥平面ACD，AC=AD=CD=DE=2a，AB=a，F为CD的中点.
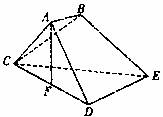
（1）求证：AF⊥平面CDE；
（2）求异面直线AC，BE所成角的余弦值；
（3）求面ACD和面BCE所成锐二面角的大小.
解：（1）∵DE⊥平面ACD，AF
平面ACD，∴DE⊥AF. 又∵AC=AD，F为CD中点，
∴AF⊥CD，∴AF⊥平面CDE.
（2）∵
DE∥AB，
取DE中点M，连结AM、CM，则四边形AMEB为平行四边形.
AM∥BE，则∠CAM为AC与BE所成的角，
在△ACM中，AC=2
，
∴异面直线AC、BE所成的角的余弦值为
.
（3）延长DA，EB交于点G，连结CG，因为AB∥DE，AB=
，所以A为GD的中点.
又因为F为CD中点，所以CG∥AF，
因为AF⊥平面CDE，所以CG⊥平面CDE，
故∠DCE为面ACD和面BCE所成二面角的平面角，易求∠DCE=45°.
练习册系列答案
阅读快车系列答案
相关题目
如图，已知多面体ABCDE中，AE⊥平面ABC，AE
如图，已知多面体ABCDE中，AB⊥平面ACD，DE⊥平面ACD，AC=AD=CD=DE=2，AB=1，F为CE的中点．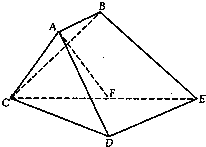
已知多面体ABCDE中，AB⊥平面ACD，DE⊥平面ACD，AC=AD=CD=DE=2，AB=1，F为CE的中点．
如图，已知多面体ABCDE中，AB⊥面ACD，DE⊥面ACD，三角形ACD是正三角形，且AD=DE=2，AB=1．
如图，已知多面体ABCDE中，AB⊥平面ACD，DE∥AB，△ACD是边长为2的正三角形，且DE=2AB=2，F是CD的中点．