题目内容
已知定义在R上的函数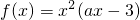 ,其中a为常数.
,其中a为常数.
(1)若x=l是函数f(x)的一个极值点,求a的值;
(2)若函数g(x)=f(x)+f′(x),x∈[0,2],在x=0处取得最大值,求正数a的取值范围.
解:(1)∵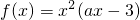 =ax3-3x2,∴f′(x)=3ax2-6x,
=ax3-3x2,∴f′(x)=3ax2-6x,
∵x=l是函数f(x)的一个极值点,∴f′(1)=0,
解得,a=2,此时f′(x)=6(x2-x)=6x(x-1),
∴当x∈(0,1)时,f′(x)<0,当x∈(-∞,0),(1,+∞)时,f′(x)>0,
∴a=2.
(2)由题意得g(x)=f(x)+f′(x)=ax3+3(a-1)x2-6x,a>0且x∈[0,2],
∴g′(x)=3ax2+6(a-1)x-6=3[ax2+2(a-1)x-2],
令g′(x)=0,即ax2+2(a-1)x-2=0,
且△=4(a-1)2+8a=4a2+4>0,
∴方程ax2+2(a-1)x-2=0有两个不同的根,设为x1,x2,则
x1x2=- <0,不妨设x1<0<x2,
<0,不妨设x1<0<x2,
当0<x2<2时,g(x2)为极小值,则g(x)在[0,2]上的最大值只能为g(0)或g(2);
当x2≥2时,则g(x)在[0,2]上是单调减函数,
∴g(x)在[0,2]上的最大值只能为g(0),
综上得,g(x)在[0,2]上的最大值只能为g(0)或g(2);
∵g(x)在x=0处取得最大值,∴g(0)≥g(2),
即0≥20a-24,得a≤ ,
,
∵a>0,∴a∈(0, ].
].
分析:(1)先求出函数f(x)的导函数f′(x),由题意f′(1)=0,解得a=2,再代入f′(x),验证在x=1处两侧的导数符号异号;
(2)由题意求出函数g(x)的导函数g′(x),再求g′(x)=0的两个根为x1,x2,再分类讨论与区间[0,2]的大小关系,求出g(x)的最大只能所有情况g(0)或g(2),根据条件列出g(0)≥g(2),代入解析式求出a的范围.
点评:本题主要考查了导数与函数的单调性,极值的关系,以及再给定区间上的最值问题,考查了分类讨论思想.
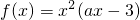 =ax3-3x2,∴f′(x)=3ax2-6x,
=ax3-3x2,∴f′(x)=3ax2-6x,∵x=l是函数f(x)的一个极值点,∴f′(1)=0,
解得,a=2,此时f′(x)=6(x2-x)=6x(x-1),
∴当x∈(0,1)时,f′(x)<0,当x∈(-∞,0),(1,+∞)时,f′(x)>0,
∴a=2.
(2)由题意得g(x)=f(x)+f′(x)=ax3+3(a-1)x2-6x,a>0且x∈[0,2],
∴g′(x)=3ax2+6(a-1)x-6=3[ax2+2(a-1)x-2],
令g′(x)=0,即ax2+2(a-1)x-2=0,
且△=4(a-1)2+8a=4a2+4>0,
∴方程ax2+2(a-1)x-2=0有两个不同的根,设为x1,x2,则
x1x2=-
 <0,不妨设x1<0<x2,
<0,不妨设x1<0<x2,当0<x2<2时,g(x2)为极小值,则g(x)在[0,2]上的最大值只能为g(0)或g(2);
当x2≥2时,则g(x)在[0,2]上是单调减函数,
∴g(x)在[0,2]上的最大值只能为g(0),
综上得,g(x)在[0,2]上的最大值只能为g(0)或g(2);
∵g(x)在x=0处取得最大值,∴g(0)≥g(2),
即0≥20a-24,得a≤
 ,
,∵a>0,∴a∈(0,
 ].
].分析:(1)先求出函数f(x)的导函数f′(x),由题意f′(1)=0,解得a=2,再代入f′(x),验证在x=1处两侧的导数符号异号;
(2)由题意求出函数g(x)的导函数g′(x),再求g′(x)=0的两个根为x1,x2,再分类讨论与区间[0,2]的大小关系,求出g(x)的最大只能所有情况g(0)或g(2),根据条件列出g(0)≥g(2),代入解析式求出a的范围.
点评:本题主要考查了导数与函数的单调性,极值的关系,以及再给定区间上的最值问题,考查了分类讨论思想.

练习册系列答案
相关题目
已知定义在R上的函数f(x),对任意x∈R,都有f(x+6)=f(x)+f(3)成立,若函数y=f(x+1)的图象关于直线x=-1对称,则f(2013)=( )
| A、0 | B、2013 | C、3 | D、-2013 |