题目内容
 如图,以棱长为a的正方体的三条棱为坐标轴,建立空间直角坐标系O-xyz,点P在正方体的对角线AB上,点Q在正方体的棱CD上.
如图,以棱长为a的正方体的三条棱为坐标轴,建立空间直角坐标系O-xyz,点P在正方体的对角线AB上,点Q在正方体的棱CD上.(1)当点P为对角线AB的中点,点Q在棱CD上运动时,探究PQ的最小值;
(2)当点P在对角线AB上运动,点Q为棱CD的中点时,探究PQ的最小值;
(3)当点P在对角线AB上运动,点Q在棱CD上运动时,探究PQ的最小值.
分析:(1)根据题意,得P(
a,
a,
a),设Q(0,a,m)(0≤m≤a),由空间两点之间的距离公式,可得PQ=
,结合二次函数的性质加以研究,可得当且仅当Q为CD的中点时PQ有最小值
a;
(2)根据题意,得Q(0,a,
a),设P(n,n,a-n)(0≤n≤a),由空间两点之间的距离公式,可得PQ=
,结合二次函数的性质加以研究,可得当且仅当P为AB的中点时,PQ的最小值为
a;
(3)设P(λ,λ,a-λ),Q(0,a,μ)(0≤λ≤a且0≤μ≤a),可得PQ关于λ、μ的表达式,用与(1)(2)类似的方法加以研究,结合二次函数的性质可得当且仅当P、Q分别为AB、CD的中点时,PQ的最小值为
a.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
|
| ||
| 2 |
(2)根据题意,得Q(0,a,
| 1 |
| 2 |
3(n-
|
| ||
| 2 |
(3)设P(λ,λ,a-λ),Q(0,a,μ)(0≤λ≤a且0≤μ≤a),可得PQ关于λ、μ的表达式,用与(1)(2)类似的方法加以研究,结合二次函数的性质可得当且仅当P、Q分别为AB、CD的中点时,PQ的最小值为
| ||
| 2 |
解答:解:∵正方体的棱长为a,∴A(a,a,0),B(0,0,a),C(0,a,0),D(0,a,a)
可得AB的中点为(
a,
a,
a),CD中点为(0,a,
a)
(1)当点P为对角线AB的中点,点Q在棱CD上运动时,
可得P(
a,
a,
a),设Q(0,a,m)(0≤m≤a)
∴PQ=
=
≥
=
a
当且仅当m=
a时,即Q为CD的中点时,PQ的最小值为
a;
(2)当P在对角线AB上运动,点Q为棱CD的中点时,
可得Q(0,a,
a),设P(n,n,a-n),(0≤n≤a)
PQ=
=
≥
=
a
当且仅当n=
a时,即P为AB的中点时,PQ的最小值为
a;
(3)设P(λ,λ,a-λ),Q(0,a,μ)(0≤λ≤a且0≤μ≤a)
可得PQ=
=
∵2(λ-
)2≥0,(a-λ-μ)2≥0,
∴2(λ-
)2+(a-λ-μ)2+
a2≥
a2,当且仅当λ-
=a-λ-μ=0时,等号成立
此时λ=μ=
a,所以当且仅当P、Q分别为AB、CD的中点时,PQ的最小值为
a.
可得AB的中点为(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(1)当点P为对角线AB的中点,点Q在棱CD上运动时,
可得P(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴PQ=
(
|
|
|
| ||
| 2 |
当且仅当m=
| 1 |
| 2 |
| ||
| 2 |
(2)当P在对角线AB上运动,点Q为棱CD的中点时,
可得Q(0,a,
| 1 |
| 2 |
PQ=
(0-n)2+(a-n)2+(
|
3(n-
|
3(
|
| ||
| 2 |
当且仅当n=
| 1 |
| 2 |
| ||
| 2 |
(3)设P(λ,λ,a-λ),Q(0,a,μ)(0≤λ≤a且0≤μ≤a)
可得PQ=
| λ2+(λ-a)2+(a-λ-μ)2 |
2(λ-
|
∵2(λ-
| a |
| 2 |
∴2(λ-
| a |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| a |
| 2 |
此时λ=μ=
| 1 |
| 2 |
| ||
| 2 |
点评:本题在正方体中求两个动点之间的距离的最小值,着重考查了空间两点之间的距离公式、二次函数的性质和正方体中的距离探索等知识,属于中档题.

练习册系列答案
相关题目
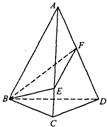 如图,已知正三棱锥A-BCD侧面的顶角为40°,侧棱长为a,动点E、F分别在侧棱AC、AD上,则以线段BE、EF、FB长度和的最小值为半径的球的体积为( )
如图,已知正三棱锥A-BCD侧面的顶角为40°,侧棱长为a,动点E、F分别在侧棱AC、AD上,则以线段BE、EF、FB长度和的最小值为半径的球的体积为( )A、4
| ||
B、
| ||
C、
| ||
| D、4πa3 |
 如图,在棱长为2的正四面体A-BCD中,若以△ABC为视角正面,则其正视图的面积是( )
如图,在棱长为2的正四面体A-BCD中,若以△ABC为视角正面,则其正视图的面积是( )











