题目内容
已知数列{an}满足: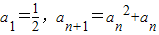 ,用[x]表示不超过x的最大整数,则
,用[x]表示不超过x的最大整数,则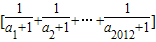 的值等于 .
的值等于 .
【答案】分析:由题意说明数列的项为正,化简数列递推关系式为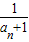 =
=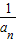 -
-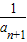 ,求出
,求出 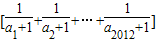 的范围,即可求出表达式的最大整数.
的范围,即可求出表达式的最大整数.
解答:解:∵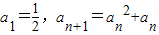 >0,所以数列是增数列,并且
>0,所以数列是增数列,并且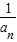 >0,
>0,
则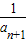 =
=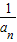 -
-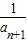 ,
,
∴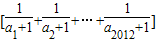
=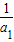 -
-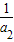 +
+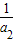 -
-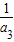 +…+
+…+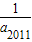 -
-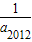 =
=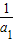 -
-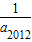 <
<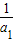 =2,
=2,
又∵a1= ,a2=
,a2= ,a3=
,a3=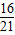 ,
,
∴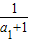 +
+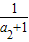 =
= +
+ >1.
>1.
∴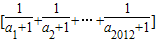 ∈(1,2).
∈(1,2).
∴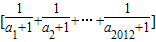 =1.
=1.
故答案为:1
点评:本题考查数列的递推关系式的应用,新定义的应用,确定表达式的取值范围是解题的关键,考查分析问题解决问题的能力,转化思想的应用.
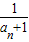 =
=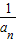 -
-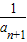 ,求出
,求出 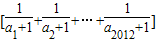 的范围,即可求出表达式的最大整数.
的范围,即可求出表达式的最大整数.解答:解:∵
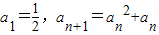 >0,所以数列是增数列,并且
>0,所以数列是增数列,并且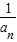 >0,
>0,则
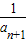 =
=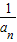 -
-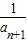 ,
,∴
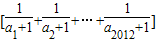
=
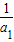 -
-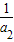 +
+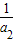 -
-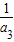 +…+
+…+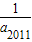 -
-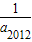 =
=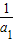 -
-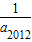 <
<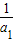 =2,
=2,又∵a1=
 ,a2=
,a2= ,a3=
,a3=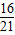 ,
,∴
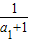 +
+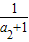 =
= +
+ >1.
>1.∴
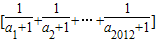 ∈(1,2).
∈(1,2).∴
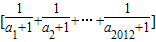 =1.
=1.故答案为:1
点评:本题考查数列的递推关系式的应用,新定义的应用,确定表达式的取值范围是解题的关键,考查分析问题解决问题的能力,转化思想的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目