题目内容
正方形ABCD的边长为2,点E、F分别在边AB、BC上,且AE=1, ,将此正方形沿DE、DF折起,使点A、C重合于点P,则三棱锥P-DEF的体积是
,将此正方形沿DE、DF折起,使点A、C重合于点P,则三棱锥P-DEF的体积是
- A.

- B.

- C.
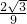
- D.

B
分析:根据已知正方形ABCD的边长为2,点E、F分别在边AB、BC上,且AE=1, ,将此正方形沿DE、DF折起,使点A、C重合于点P,可知DP⊥PE,DP⊥PF,PE∩PF=P,故得到DP⊥面PEF,因此要求三棱锥P-DEF的体积,即求三棱锥D-PEF的体积,利用余弦定理求得cos∠PEF=0,进而求得sin∠PEF,利用三角形面积公式求得
,将此正方形沿DE、DF折起,使点A、C重合于点P,可知DP⊥PE,DP⊥PF,PE∩PF=P,故得到DP⊥面PEF,因此要求三棱锥P-DEF的体积,即求三棱锥D-PEF的体积,利用余弦定理求得cos∠PEF=0,进而求得sin∠PEF,利用三角形面积公式求得 ,代入体积公式即可求得结论.
,代入体积公式即可求得结论.
解答:根据题意知DP⊥PE,DP⊥PF,PE∩PF=P,
∴DP⊥面PEF,
而DP=2,EF= ,PE=1,PF=
,PE=1,PF= ,
,
由余弦定理得cos∠PEF= =0,
=0,
∴sin∠PEF=1,∴ =
= ,
,
∴VP-DEF=VD-PEF= ,
,
故选B. ?
?
点评:此题是中档题.本题主要考查了折叠问题,解决此题的关键是抓住折叠前后不变的量解决问题,考查空间想象能力、运算能力和推理论证能力.
分析:根据已知正方形ABCD的边长为2,点E、F分别在边AB、BC上,且AE=1,
 ,将此正方形沿DE、DF折起,使点A、C重合于点P,可知DP⊥PE,DP⊥PF,PE∩PF=P,故得到DP⊥面PEF,因此要求三棱锥P-DEF的体积,即求三棱锥D-PEF的体积,利用余弦定理求得cos∠PEF=0,进而求得sin∠PEF,利用三角形面积公式求得
,将此正方形沿DE、DF折起,使点A、C重合于点P,可知DP⊥PE,DP⊥PF,PE∩PF=P,故得到DP⊥面PEF,因此要求三棱锥P-DEF的体积,即求三棱锥D-PEF的体积,利用余弦定理求得cos∠PEF=0,进而求得sin∠PEF,利用三角形面积公式求得 ,代入体积公式即可求得结论.
,代入体积公式即可求得结论.解答:根据题意知DP⊥PE,DP⊥PF,PE∩PF=P,
∴DP⊥面PEF,
而DP=2,EF=
 ,PE=1,PF=
,PE=1,PF= ,
,由余弦定理得cos∠PEF=
 =0,
=0,∴sin∠PEF=1,∴
 =
= ,
,∴VP-DEF=VD-PEF=
 ,
,故选B.
 ?
?
点评:此题是中档题.本题主要考查了折叠问题,解决此题的关键是抓住折叠前后不变的量解决问题,考查空间想象能力、运算能力和推理论证能力.

练习册系列答案
相关题目
 如图,正方形ABCD的边长为1,正方形ADEF所在平面与平面ABCD互相垂直,G,H是DF,FC的中点.
如图,正方形ABCD的边长为1,正方形ADEF所在平面与平面ABCD互相垂直,G,H是DF,FC的中点.