题目内容
已知一个直角三角形的周长为 ,斜边上的中线长为2,则该直角三角形的面积为
,斜边上的中线长为2,则该直角三角形的面积为
- A.

- B.

- C.

- D.

B
分析:由题意构造直角三角形,令∠ACB=90°,CD是斜边上的中线,求出AB=4,根据AB+AC+BC= ,求出AC+BC,根据勾股定理得出AC2+BC2=AB2=16,推出AC•BC=14,根据S=
,求出AC+BC,根据勾股定理得出AC2+BC2=AB2=16,推出AC•BC=14,根据S= AC•BC即可求出答案.
AC•BC即可求出答案.
解答: 解:由题意构造直角三角形如图,令∠ACB=90°,CD是斜边上的中线,
解:由题意构造直角三角形如图,令∠ACB=90°,CD是斜边上的中线,
∴AB=2CD=4,
∵AB+AC+BC= ,
,
∴AC+BC=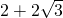 ,
,
由勾股定理得:AC2+BC2=AB2=16,
∴(AC+BC)2-2AC•BC=16,
AC•BC=4 ,
,
∴S= AC•BC=
AC•BC= =
= .
.
故选B.
点评:本题考查直角三角形斜边上的中线,勾股定理,三角形的面积等知识点的理解和掌握,巧妙求出AC•BC的值是解此题的关键,值得学习应用.
分析:由题意构造直角三角形,令∠ACB=90°,CD是斜边上的中线,求出AB=4,根据AB+AC+BC=
 ,求出AC+BC,根据勾股定理得出AC2+BC2=AB2=16,推出AC•BC=14,根据S=
,求出AC+BC,根据勾股定理得出AC2+BC2=AB2=16,推出AC•BC=14,根据S= AC•BC即可求出答案.
AC•BC即可求出答案.解答:
 解:由题意构造直角三角形如图,令∠ACB=90°,CD是斜边上的中线,
解:由题意构造直角三角形如图,令∠ACB=90°,CD是斜边上的中线,∴AB=2CD=4,
∵AB+AC+BC=
 ,
,∴AC+BC=
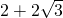 ,
,由勾股定理得:AC2+BC2=AB2=16,
∴(AC+BC)2-2AC•BC=16,
AC•BC=4
 ,
,∴S=
 AC•BC=
AC•BC= =
= .
.故选B.
点评:本题考查直角三角形斜边上的中线,勾股定理,三角形的面积等知识点的理解和掌握,巧妙求出AC•BC的值是解此题的关键,值得学习应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的两根,则这个直角三角形的斜边长等于( )
的两根,则这个直角三角形的斜边长等于( ) B.3 C.6 D.9
B.3 C.6 D.9