Question

（本小题满分12分）

已知函数f(x)=x²-alnx在（1,2]上是增函数，g(x)=x-a 在（0,1）上为减函数；

（1）求f(x)、g(x)的表达式；

（2）求证：当x＞0 时，方程f(x)=g(x)+2有唯一解；

（3）当b＞-1时，若f(x)≥2bx-对0＜x≤1恒成立，求b的取值范围。

Answer 1

解: 解：（1）∵f(x)在（1,2]上是增函数, ∴对恒成立

2x-≥0对恒成立,

∵g(x)在（0,1）上是减函数, ∴对恒成立对恒成立，

∴ a=2，即：f(x)=x²-2lnx，g(x)=x-2------------------------------------4分

（2）f(x)=g(x)+2

∵

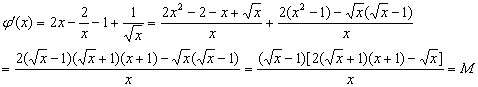
∴x＞1时，M＞0,x＜1时，M＜0，

∴--------------------------7分

（3）对恒成立对恒成立。

∵，

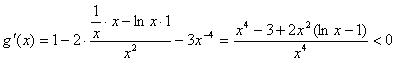∴g(x)在（0,1]递减，∴2b≤g(x)_最小值=g(1)=2，即b≤1，有b＞-1

∴b的取值范围为（-1,1]。------------------------------------------------12分