题目内容
已知直线l1方程为x+y-3=0与x轴交于点A,直线l2方程是y=2x,l2与l1交于点B,点C在y轴负半轴上,AC=2
.
(1)写出点A、B、C的坐标;
(2)求△ABC的面积;
(3)求△ABC外接圆方程.
| 3 |
(1)写出点A、B、C的坐标;
(2)求△ABC的面积;
(3)求△ABC外接圆方程.
分析:(1)对于直线l1方程为x+y-3=0,令y=0,解得x,即可得到A.联立
,解得B.设C(0,y)(y<0),利用两点间的距离公式及|AC|=2
,解得y即可.
(2)利用点斜式可得直线AC的方程,再利用点到直线的距离公式可得点B到直线AC的距离d,即可得到S△ABC=
|AC|•d
(3)设△ABC外接圆方程为x2+y2+Dx+Ey+F=0,把A(3,0),B(1,2),C(0,-
)代入得解出即可.
|
| 3 |
(2)利用点斜式可得直线AC的方程,再利用点到直线的距离公式可得点B到直线AC的距离d,即可得到S△ABC=
| 1 |
| 2 |
(3)设△ABC外接圆方程为x2+y2+Dx+Ey+F=0,把A(3,0),B(1,2),C(0,-
| 3 |
解答:解:(1)对于直线l1方程为x+y-3=0,令y=0,解得x=3,∴A(3,0).
联立
,解得
,∴B(1,2).
设C(0,y)(y<0),∵|AC|=2
,∴
=2
,解得y=-
,∴C(0,-
).
(2)直线AC的方程为y=
x-
,化为x-
y-1=0,
点B到直线AC的距离d=
=
,
∴S△ABC=
|AC|•d=
×2
×
=3.
(3)设△ABC外接圆方程为x2+y2+Dx+Ey+F=0,把A(3,0),B(1,2),C(0,-
)代入得
,解得D=-3,E=2-
,F=2
-6.
∴△ABC外接圆方程为x2+y2-3x+(2-
)y+2
-6=0.
联立
|
|
设C(0,y)(y<0),∵|AC|=2
| 3 |
| 32+y2 |
| 3 |
| 3 |
| 3 |
(2)直线AC的方程为y=
0+
| ||
| 3-0 |
| 3 |
| 3 |
点B到直线AC的距离d=
|1-2
| ||||
|
| 3 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
(3)设△ABC外接圆方程为x2+y2+Dx+Ey+F=0,把A(3,0),B(1,2),C(0,-
| 3 |
|
| 3 |
| 3 |
∴△ABC外接圆方程为x2+y2-3x+(2-
| 3 |
| 3 |
点评:熟练掌握直线的交点与方程联立的关系、点到直线的距离公式、三角形的面积计算公式、三角形外接圆的一般式方程等是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
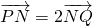 ,求直线L的方程.
,求直线L的方程.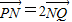 ,求直线L的方程.
,求直线L的方程.