题目内容
直线y=2x+5与曲线| x|x| |
| 9 |
| y2 |
| 25 |
分析:先判断曲线
+
=1形状,当x<0时,是双曲线上支,当x>0是椭圆y轴右侧部分,再让直线方程分别与两种曲线方程联立,根据方程组的解判断.
| x|x| |
| 9 |
| y2 |
| 25 |
解答:解:若x≤0 由
得,x1=0或x2=-5,均满足题意,即直线与半双曲线有两个交点;
若x>0由
得 x=0,等同于故此种情况无解
综上所述交点个数有两个,
故答案为:2个
|
若x>0由
|
综上所述交点个数有两个,
故答案为:2个
点评:本题考查直线与圆锥曲线的位置关系,解决的方法是分类讨论法,解方程组,体现的数学思想有转化思想,方程思想,也可以用数形结合法解决.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
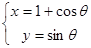 ,直线l:y=2x+b,那么曲C与直线l相切的充要条件是
,直线l:y=2x+b,那么曲C与直线l相切的充要条件是 B.b=-
B.b=-