题目内容
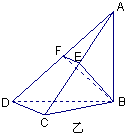
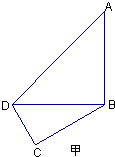
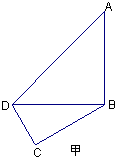
如图甲，在平面四边形ABCD中，已知∠A＝45°，∠C＝90°，∠ADC＝105°，AB＝BD，现将四边形ABCD沿BD折起，使平面ABD⊥平面BDC(如图乙)，设点E、F分别为棱AC、AD的中点．
(Ⅰ)求证：DC⊥平面ABC；
(Ⅱ)设CD＝a，求三棱锥A－BFE的体积．
答案：
解析：
解析：
|
(Ⅰ)证明：在图甲中∵ 即 在图乙中，∵平面ABD ∴AB⊥底面BDC，∴AB⊥CD． 又 ∴DC (Ⅱ)解：∵E、F分别为AC、AD的中点 ∴EF//CD，又由(Ⅰ)知，DC ∴EF⊥平面ABC， |
且
∴
，
平面BDC，且平面ABD
平面BDC＝BD
，∴DC⊥BC，且
平面ABC．
平面ABC，
练习册系列答案
相关题目
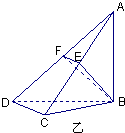
如图甲，在平面四边形ABCD中，已知∠A=45°，∠C=90°，∠ADC=105°，AB=BD，现将四边形ABCD沿BD折起，使平面ABD⊥平面BDC（如图乙），设点E、F分别为棱AC、AD的中点．
如图甲，在平面四边形ABCD中，已知∠A=45°，∠C=90°，∠ADC=105°，AB=BD，现将四边形ABCD沿BD折起，使平面ABD⊥平面BDC（如图乙），设点E、F分别为棱AC、AD的中点．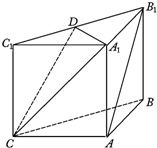
如图，在三棱柱ABC-A1B1C1中，侧面ABB1A1，ACC1A1均为正方形，∠BAC=90°，点D是棱B1C1的中点．
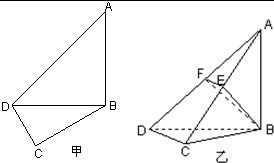在平面四边形ABCD中，已知∠A=45°，∠C=90°，∠ADC=105°，AB=BD，现将四边形ABCD沿BD折起，使平面ABD⊥平面BDC（如图乙），设点E、F分别为棱AC、AD的中点．
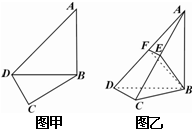如图甲，在平面四边形ABCD中，已知∠A=45°，∠C=90°，∠ADC=105°，AB=BD，现将四边形ABCD沿BD折起，使平面ABD⊥平面BDC（如图乙），设点E、F分别为棱AC、AD的中点．
如图甲，在平面四边形ABCD中，已知∠A=45°，∠C=90°，AB=BD=2CD，现将四边形ABCD沿BD折起，使平面ABD⊥平面BDC（如图乙），设点E为棱AD的中点．