题目内容

设关于x的方程2x2－ax－2＝0的两根分别为α、β(α＜β)，函数

(1)证明f(x)在区间(α，β)上是增函数；

(2)当a为何值时，f(x)在区间[α，β]上的最大值与最小值之差最小

答案：
解析：

　　(1)证明：，

　　由方程的两根分别为、知

　　时，，所以此时，

　　所以在区间上是增函数

　　(2)解：由(1)知在上，最小值为，最大值为，

　　

　　，，可求得，

　　，

　　所以当时，在区间上的最大值与最小值之差最小，最小值为4


练习册系列答案
相关题目
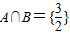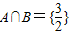设关于x的方程2x2-ax-2=0的两根为α、β（α＜β），函数f(x)=
4x-ax2+1
．
（1）求f（α）、f（β）的值；
（2）证明f（x）是[α，β]上的增函数；
（3）当α为何值时，f（x）在区间[α，β]上的最大值与最小值之差最小？
设关于x的方程2x2+ax-9=0，bx2+x-6=0的解集分别为A、B，且A∩B={
32
}．
（Ⅰ） 求a和b的值；
（Ⅱ） 求函数f（x）=ax2+bx-8的零点．
设关于x的方程2x2-ax-2=0的两根为α，β（α＜β），函数f(x)=
4x-ax2+1
，且|f（α）•f（β）|=4．
（1）证明：f（x）在[α，β]上是增函数；
（2）当α为何值时，f（x）在[α，β]上的最大值与最小值之差最小？
设关于x的方程2x2+ax-9=0，bx2+x-6=0的解集分别为A、B，且．
（Ⅰ） 求a和b的值；
（Ⅱ） 求函数f（x）=ax2+bx-8的零点．
设关于x的方程2x2+ax-9=0，bx2+x-6=0的解集分别为A、B，且．
（Ⅰ） 求a和b的值；
（Ⅱ） 求函数f（x）=ax2+bx-8的零点．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网