题目内容
设函数![]() ,数列
,数列![]() 满足
满足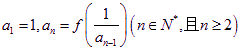 .
.
⑴求数列![]() 的通项公式;
的通项公式;
⑵设![]() ,若
,若![]() 对
对![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
⑶是否存在以![]() 为首项,公比为
为首项,公比为![]() 的数列
的数列![]() ,
,![]() ,使得数列
,使得数列![]() 中每一项都是数列
中每一项都是数列![]() 中不同的项,若存在,求出所有满足条件的数列
中不同的项,若存在,求出所有满足条件的数列![]() 的通项公式;若不存在,说明理由
的通项公式;若不存在,说明理由
(1) ![]() (2)
(2) ![]() (3)
(3) ![]()
解析:
⑴因为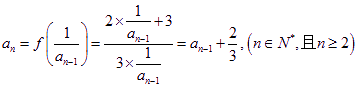 ,
,
所以![]() .…………………………………………………………………………2分
.…………………………………………………………………………2分
因为![]() ,所以数列
,所以数列![]() 是以1为首项,公差为
是以1为首项,公差为![]() 的等差数列.
的等差数列.
所以![]() .…………………………………………………………………………4分
.…………………………………………………………………………4分
⑵①当![]() 时,
时,
![]()
![]()
![]()
![]()
![]() .…………………………………………………………………………6分
.…………………………………………………………………………6分
②当![]() 时,
时,
![]()
![]()
![]() .…………………………………………8分
.…………………………………………8分
所以
要使![]() 对
对![]() 恒成立,
恒成立,
只要使![]() .
.
只要使![]() ,
,
故实数![]() 的取值范围为
的取值范围为![]() .……………………………………………………10分
.……………………………………………………10分
⑶由![]() ,知数列
,知数列![]() 中每一项都不可能是偶数.
中每一项都不可能是偶数.
①如存在以![]() 为首项,公比
为首项,公比![]() 为2或4的数列
为2或4的数列![]() ,
,![]() ,
,
此时![]() 中每一项除第一项外都是偶数,故不存在以
中每一项除第一项外都是偶数,故不存在以![]() 为首项,公比为偶数的数列
为首项,公比为偶数的数列![]() .……………………………………………………………………………………12分
.……………………………………………………………………………………12分
②当![]() 时,显然不存在这样的数列
时,显然不存在这样的数列![]() .
.
当![]() 时,若存在以
时,若存在以![]() 为首项,公比为3的数列
为首项,公比为3的数列![]() ,
,![]() .
.
则![]() ,
,![]() ,
,![]() ,
,![]() .
.
所以满足条件的数列![]() 的通项公式为
的通项公式为![]() .……………………………16分
.……………………………16分

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
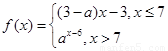 ,数列
,数列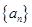 满足
满足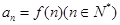 ,且数列
,且数列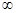 )
D. (2, +
)
D. (2, +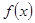 与数列
与数列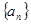 满足关系:(1) a1.>a, 其中a是方程
满足关系:(1) a1.>a, 其中a是方程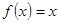 的实根,(2) an+1=
的实根,(2) an+1= ( n
( n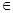 N+
) ,如果
N+
) ,如果 <1
<1  ,数列
,数列 满足
满足 ,且数列
,且数列 的取值范围是_____________________________。
的取值范围是_____________________________。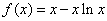 .数列
.数列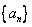 满足
满足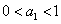 ,
,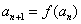 .
.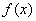 在区间
在区间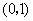 是增函数;
是增函数;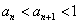 ;
;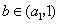 ,整数
,整数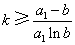 .证明:
.证明: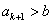 .
.