题目内容
4.已知f(x)=x3+ax2+bx+c,若f(x)在(-1,0)上单调递减,则a2+b2的取值范围为$[{\frac{9}{5},+∞})$.分析 由题意可知f′(x)≤0在(-1,0)上恒成立,从而结合f′(x)=3x2+2ax+b的图象开口向上可得不等式组$\left\{\begin{array}{l}{f′(-1)=3-2a+b≤0}\\{f′(0)=b≤0}\end{array}\right.$,从而转化为线性规划问题求解即可.
解答 解:∵f(x)=x3+ax2+bx+c,
∴f′(x)=3x2+2ax+b,
∵f(x)在(-1,0)上单调递减,
∴f′(x)≤0在(-1,0)上恒成立,
∵f′(x)=3x2+2ax+b的图象开口向上,
∴$\left\{\begin{array}{l}{f′(-1)=3-2a+b≤0}\\{f′(0)=b≤0}\end{array}\right.$,
作不等式组表示的平面区域如下,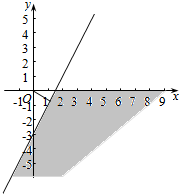 ,
,
a2+b2的几何意义是阴影内的点与原点的距离的平方,
且原点到直线3-2a+b=0的距离的平方为
$\frac{|3-0{|}^{2}}{{2}^{2}+1}$=$\frac{9}{5}$;
故a2+b2≥$\frac{9}{5}$;
故答案为:$[{\frac{9}{5},+∞})$.
点评 本题考查了导数与不等式的综合应用,同时考查了a2+b2的几何意义的应用,综合性较强.

练习册系列答案
相关题目
9.已知Sn是数列{an}的前n项和,a1=1,a2=2,a3=3,数列{an+an+1+an+2}是公差为2的等差数列,则S25=( )
| A. | 232 | B. | 233 | C. | 234 | D. | 235 |
16.在区间[-3,3]上随机取一个实数a,能使函数f(x)=x2+2x+a-1在R上有零点的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{5}{6}$ |
13.已知复数z=$\frac{1}{1-i}$+i,则复数z的模|z|=( )
| A. | $\sqrt{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{10}$ | D. | $\frac{\sqrt{10}}{2}$ |